题目内容
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
【答案】B
【解析】解:根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD,连接OP,OQ,过Q作QM⊥y轴,
∴∠POQ=120°,
∵AP=OP,
∴∠BAO=∠POA=30°,
∴∠MOQ=30°,
在Rt△OMQ中,OQ=OP=2,
∴MQ=1,OM= ![]() ,
,
则P的对应点Q的坐标为(1,﹣ ![]() ),
),
故选B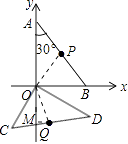
根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD,连接OP,OQ,过Q作QM⊥y轴,由旋转的性质得到∠POQ=120°,根据AP=BP=OP=2,得到∠AOP度数,进而求出∠MOQ度数为30°,在直角三角形OMQ中求出OM与MQ的长,即可确定出Q的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

