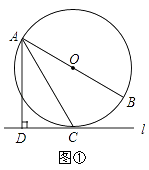题目内容
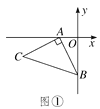
【题目】如图①,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
(1)求C点的坐标;
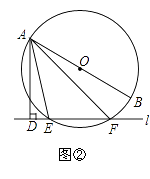
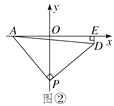
(2)如图②,OA=2,P为y轴负半轴上一个动点,当P点在y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值.
【答案】(1)点C的坐标为(-6,-2);(2)OP-DE=2.
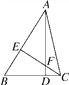
【解析】(1)如图1,过C作CM⊥x轴于M点,则可以求出△MAC≌△OBA,可得CM=OA=2,MA=OB=4,故点C的坐标为(-6,-2).
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ利用三角形全等的判定定理可得△AOP≌△PQD(AAS)进一步可得PQ=OA=2,即OP-DE=2.
(1)如图①,过C作CM⊥x轴于M点,
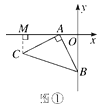
则∠CMA=90°.
∵△ABC为等腰直角三角形,且∠AOB=90°,
∴∠BAC=90°,AC=BA,
∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,则∠MAC=∠OBA.
在△MAC和△OBA中,
∠CMA=∠AOB,∠MAC=∠OBA,AC=BA,
∴△MAC≌△OBA(AAS),
∴CM=OA=2,MA=OB=4,
∴OM=OA+AM=2+4=6,
∴点C的坐标为(-6,-2).
(2)如图②,过D作DQ⊥OP于Q点,
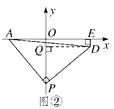
则∠PQD=90°,DE=OQ,
∴OP-DE=OP-OQ=PQ.
∵△APD为等腰直角三角形,且∠AOP=90°,
∴∠APD=90°,AP=PD,∴∠APO+∠QPD=90°,∠APO+∠OAP=90°,
∴∠QPD=∠OAP.
在△AOP和△PQD中,
∠AOP=∠PQD,∠QPD=∠OAP,AP=PD,
∴△AOP≌△PQD(AAS).
∴PQ=OA=2.即OP-DE=2.

【题目】阅读下面材料:在数学课上,老师提出如下问题:
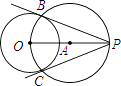
尺规作图,过圆外一点作圆的切线. |
小涵的主要作法如下:
如图,(1)连结OP,作线段OP的中点A; |
老师说:“小涵的做法是正确的.”
请回答:小涵的作图依据是 .