题目内容
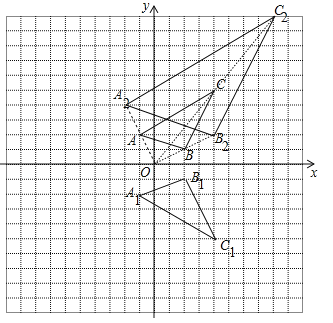
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.

【答案】(1)作图见解析;(2)作图见解析,28.
【解析】试题分析:(1)画出A、B、C关于x轴的对称点A1、B1、C1即可解决问题;
(2)连接OB延长OB到B2,使得OB=BB2,同法可得A2、C2,△A2B2C2就是所求三角形;
试题解析:解:(1)如图所示,△A1B1C1就是所求三角形;
(2)如图所示,△A2B2C2就是所求三角形.
如图,分别过点A2、C2作y轴的平行线,过点B2作x轴的平行线,交点分别为E、F,∵A(﹣1,2),B(2,1),C(4,5),△A2B2C2与△ABC位似,且位似比为2,∴A2(﹣2,4),B2(4,2),C2(8,10),∴![]() =8×10﹣
=8×10﹣![]() ×6×2﹣
×6×2﹣![]() ×4×8﹣
×4×8﹣![]() ×6×10=28.
×6×10=28.

练习册系列答案
相关题目

