Question

【题目】在中，，是平面内不与点重合的任意一点，连接，将线段绕点顺时针旋转得到线段，连接是的中点，是的中点．

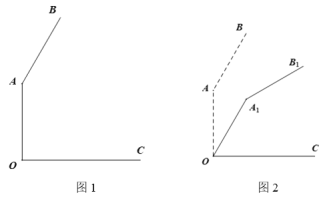
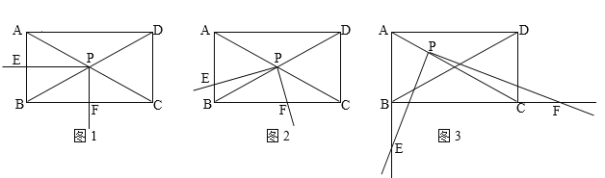
（1）问题发现：

如图1，当时，的值是_________，直线与直线相交所成的较小角的度数是________．

（2）类比探究：

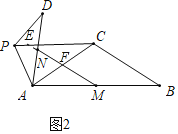
如图2，当时，请写出的值及直线与直线相交所成的较小角的度数，并说明理由．

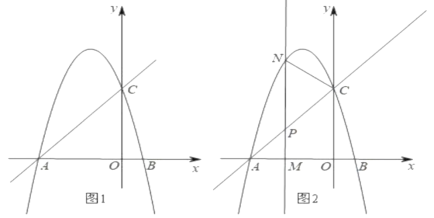
（3）解决问题：

如图3，当时，若是的中点，点在直线上，且点在同一条直线上，请直接写出的值．

Answer 1

【答案】（1），；（2），，见解析；（3）的值是或

【解析】

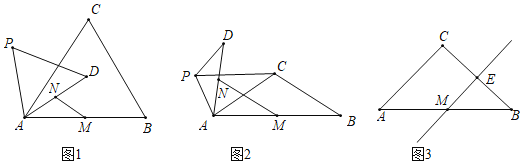
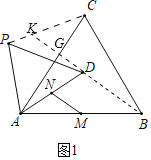
（1）如图1中，连接PC，BD，延长BD交PC于K，交AC于G．证明△PAC≌△DAB（SAS），利用全等三角形的性质以及三角形的中位线定理即可解决问题．
（2）如图2，设MN交AC于F，延长MN交PC于E．证明△ACP∽△AMN，推出∠ACP=∠AMN，可得结论；

（3）分两种情形分别画出图形，利用三角形中位线定理即可解决问题．

解：（1），

如图1，连接并延长交于点，交于点，

，

均是等边三角形，

，

，

在△PAC和△DAB中，

，

，

，

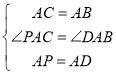是的中点，是的中点，是的中位线，

，

，

，

，

与相交所成的较小角的度数是，

，

与相交所成的较小角的度数是；

（2），直线与直线相交所成的较小角的度数是，

理由：如图2，设交于点，延长交于点，连接，

，

，

，

，

，

，

，

，

，

，

，

即直线与直线相交所成的较小角的度数是；

（3）或

设，由（2）易知，，

，

是的中位线，，

是线段的中垂线，

，

是的中位线，

，

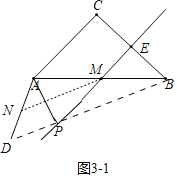
如图3-1，当点在线段上时，，

，

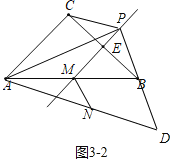
如3-2图，当点在直线上但不在线段上时，

；

综上，的值是或.