题目内容
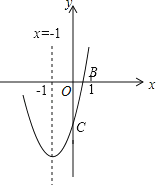
【题目】已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc>0;②2a﹣b=0;③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大:⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
A.5B.4C.3D.2
【答案】C
【解析】
根据抛物线的开口方向、对称轴、顶点坐标、增减性逐个进行判断,得出答案.
由抛物线的开口向上,可得a>0,对称轴是x=﹣1,可得a、b同号,即b>0,抛物线与y轴交在y轴的负半轴,c<0,因此abc<0,故①不符合题意;
对称轴是x=﹣1,即﹣![]() =﹣1,即2a﹣b=0,因此②符合题意;
=﹣1,即2a﹣b=0,因此②符合题意;
抛物线的对称轴为x=﹣1,与x轴的一个交点B的坐标为(1,0),可知与x轴的另一个交点为(﹣3,0),因此一元二次方程ax2+bx+c=0的两个根是﹣3和1,故③符合题意;
由图象可知y>0时,相应的x的取值范围为x<﹣3或x>1,因此④不符合题意;
在对称轴的右侧,y随x的增大而增大,因此当x>0时,y随x的增大而增大是正确的,因此⑤符合题意;
由抛物线的对称性,在对称轴的左侧y随x的增大而减小,
∵﹣4<﹣2,
∴y1>y2,(3,y3)l离对称轴远
因此y3>y1,因此y3>y1>y2,因此⑥不符合题意;
综上所述,正确的结论有3个,
故选:C.

【题目】某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
学生能接受的早餐价格统计表
价格分组(单位:元) | 频数 | 频率 |
0<x≤2 | 60 | 0.15 |
2<x≤4 | 180 | c |
4<x≤6 | 92 | 0.23 |
6<x≤8 | a | 0.12 |
x>8 | 20 | 0.05 |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a= ,b= ,c= .
(2)扇形统计图中,m的值为 ,“甜”所对应的圆心角的度数是 .
(3)该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?