Question

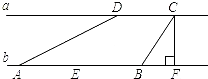
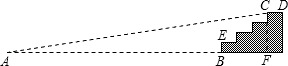
某商场门前的台阶截面如图所示．已知每级台阶的宽度（如CD）均为30cm，高度（如BE）均为20cm．为了方便残疾人行走，商场决定将其中一个门的门前台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角为9度．请计算从斜坡起点A到台阶前的点B的水平距离．
（参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0.16）

Answer 1

过C作CF⊥AB，交AB的延长线于点F．
由条件，得CF=80cm，BF=90cm．（1分）
在Rt△CAF中，tanA=

CF

AF

．（2分）
∴AF=

CF

tan9°

≈

80

0.16

=500．（4分）
∴AB=AF-BF=500-90=410（cm）．（5分）
答：从斜坡起点A到台阶前点B的距离为410cm．（6分）