题目内容
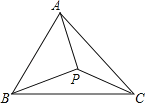
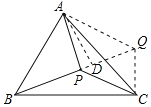
【题目】如图,等边△ABC中,AB=![]() ,3BP=4CP,∠BPC=120°,那么线段AP的长度是_____.
,3BP=4CP,∠BPC=120°,那么线段AP的长度是_____.
【答案】![]() .
.
【解析】
延长BP至Q,使PQ=PC,连接QA、QC,作AD⊥PQ于D,证明△PCQ是等边三角形,得出∠PCQ=∠PQC=60°,QC=PC,证出∠ACQ=∠BCP,证明△ACQ≌△BCP(SAS),得出AQ=BP,∠AQC=∠BPC=120°,得出∠AQP=120°﹣60°=60°,由直角三角形的性质得出DQ=![]() AQ,AD=
AQ,AD=![]() DQ.设PQ=PC=3a,则AQ=BP=4a,得出DQ=2a,AD=2
DQ.设PQ=PC=3a,则AQ=BP=4a,得出DQ=2a,AD=2![]() a,PD=PQ﹣DQ=a,BD=BP+PD=5a,在Rt△ABD中,由勾股定理得出方程,得出PD=1,AD=2
a,PD=PQ﹣DQ=a,BD=BP+PD=5a,在Rt△ABD中,由勾股定理得出方程,得出PD=1,AD=2![]() ,由勾股定理即可得出答案.
,由勾股定理即可得出答案.
延长BP至Q,使PQ=PC,连接QA、QC,作AD⊥PQ于D,如图所示:
∵∠BPC=120°,
∴∠CPQ=60°,
∵PQ=PC,
∴△PCQ是等边三角形,
∴∠PCQ=∠PQC=60°,QC=PC,
∵△ABC是等边三角形,
∴BC=AC=AB=![]() ,∠ACB=60°,
,∠ACB=60°,
∴∠ACQ=∠BCP,
在△ACQ和△BCP中,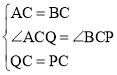 ,
,
∴△ACQ≌△BCP(SAS),
∴AQ=BP,∠AQC=∠BPC=120°,
∴∠AQP=120°﹣60°=60°,
∵AD⊥PQ,
∴∠QAD=30°,
∴DQ=![]() AQ,AD=
AQ,AD=![]() DQ,
DQ,
∵3BP=4CP,
∴设PQ=PC=3a,则AQ=BP=4a,
∴DQ=2a,AD=2![]() a,
a,
∴PD=PQ﹣DQ=a,
∴BD=BP+PD=5a,
在Rt△ABD中,由勾股定理得:(5a)2+(2![]() a)2=(
a)2=(![]() )2,
)2,
解得:a=1,
∴PD=1,AD=2![]() ,
,
∴AP=![]() =
=![]() =
=![]() ;
;
故答案为:![]() .
.

练习册系列答案
相关题目