Question

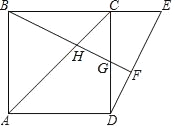
【题目】如图，点E是正方形ABCD的边BC延长线上一点，联结DE，过顶点B作BF⊥DE，垂足为F，BF交边DC于点G．

（1）求证：GDAB=DFBG；

（2）联结CF，求证：∠CFB=45°．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）先证明△BGC∽△DGF，然后根据相似三角形的性质列比例式整理即可；（2）连接BD、CF，由△BGC∽△DGF，可得,变形得，可证△BGD∽△CGF，从而∠BDG=∠CFG，再根据正方形的性质求出∠BDG即可.

证明：（1）∵四边形ABCD是正方形

∴∠BCD=∠ADC=90°，AB=BC，

∵BF⊥DE，

∴∠GFD=90°，

∴∠BCD=∠GFD，

∵∠BGC=∠FGD，

∴△BGC∽△DGF，

∴，

∴DGBC=DFBG，

∵AB=BC，

∴DGAB=DFBG；

（2）如图，连接BD、CF，

∵△BGC∽△DGF，

∴，

∴，

又∵∠BGD=∠CGF，

∴△BGD∽△CGF，

∴∠BDG=∠CFG，

∵四边形ABCD是正方形，BD是对角线，

∴，

∴∠CFG=45°．