Question

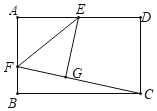
【题目】如图，矩形ABCD中，AB=，BC=12，E为AD中点，F为AB上一点，将△AEF沿EF折叠后，点A恰好落到CF上的点G处，则折痕EF的长是_______ .

Answer 1

【答案】

【解析】

连接EC，利用矩形的性质，求出EG，DE的长度，证明EC平分∠DCF，再证∠FEC=90°，最后证△FEC∽△EDC，利用相似的性质即可求出EF的长度．

解：如图，连接EC，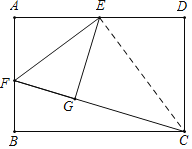

∵四边形ABCD为矩形，
∴∠A=∠D=90°，BC=AD=12，DC=AB=

∵E为AD中点，
∴AE=DE=

由翻折知，△AEF≌△GEF，
∴AE=GE=6，∠AEF=∠GEF，∠EGF=∠EAF=90°=∠D，
∴GE=DE，
∴EC平分∠DCG，
∴∠DCE=∠GCE，
∵∠GEC=90°-∠GCE，∠DEC=90°-∠DCE，
∴∠GEC=∠DEC，
∴∠FEC=∠FEG+∠GEC= ×180°=90°，
∴∠FEC=∠D=90°，
又∵∠DCE=∠GCE，
∴△FEC∽△EDC，

故答案为：