ЬтФПФкШн
ЁОЬтФПЁПвбжЊХзЮяЯпC1ЃКyЃНax2+bx+b2ЯђзѓЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНХзЮяЯпC2ЃКyЃНx2.
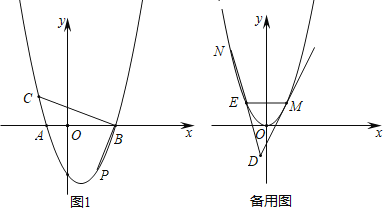
ЃЈ1ЃЉжБНгаДГіХзЮяЯпC1ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌвбжЊХзЮяЯпC1НЛxжсгкЕуAЁЂЕуBЃЌЕуAдкЕуBЕФзѓВрЃЌЕуPЃЈ2ЃЌtЃЉдкХзЮяЯпC1ЩЯЃЌCBЁЭPBНЛХзЮяЯпгкЕуCЃЌЧѓCЕуЕФзјБъЃЛ
ЃЈ3ЃЉвбжЊЕуEЁЂЕуMдкХзЮяЯпC2ЩЯЃЌEMЁЮxжсЃЌЕуEдкЕуMзѓВрЃЌЙ§ЕуMЕФжБЯпMDгыХзЮяЯпC2жЛгавЛИіЙЋЙВЕуЃЈMDгыyжсВЛЦНааЃЉЃЌжБЯпDEгыХзЮяЯпНЛгкСэвЛЕуNЃЎШєЯпЖЮNEЃНDEЃЌЩшЕуMЁЂNЕФКсзјБъЗжБ№ЮЊmЁЂnЃЌЧѓmКЭnЕФЪ§СПЙиЯЕЃЈгУКЌmЕФЪНзгБэЪОnЃЉ
ЁОД№АИЁПЃЈ1ЃЉyЃНЃЈxЉ1ЃЉ2Љ4ЃЛЃЈ2ЃЉCЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉnЃНЃЈ1
ЃЉЃЛЃЈ3ЃЉnЃНЃЈ1![]() ЃЉmЃЎ
ЃЉmЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉХзЮяЯпC2ЃКyЃНx2ЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНC1ЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЙ§ЕуBзїyжсЕФЦНааЯпMNЃЌЙ§ЕуCзїCMЁЭMNгкЕуMЃЌЙ§ЕуPзїPNЁЭMNгкЕуNЃЌжЄУїЁЯBCMЃНЁЯPBNЃЌдђtanЁЯMCBЃНtanЁЯPBNЃН![]() ЃЌЩшBMЃНmЃЌдђCMЃН3mЃЌПЩЕУЕуCЃЈ3Љ3mЃЌmЃЉЃЌНЋЕуCЕФзјБъДњШыC1ЕФНтЮіЪНЃЌМДПЩЧѓНтЃЛ
ЃЌЩшBMЃНmЃЌдђCMЃН3mЃЌПЩЕУЕуCЃЈ3Љ3mЃЌmЃЉЃЌНЋЕуCЕФзјБъДњШыC1ЕФНтЮіЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉгЩЬтвтПЩЕУЕуMЁЂNЕФзјБъЮЊЃКЃЈmЃЌm2ЃЉЁЂЃЈnЃЌn2ЃЉЃЌЕуEЃЈЉmЃЌm2ЃЉЃЌЩшжБЯпMDЕФБэДяЪНЮЊЃКyЃНkx+bЃЌДњШыЕуMЕФзјБъВЂИљОнжБЯпMDгыХзЮяЯпC2жЛгавЛИіЙЋЙВЕуПЩЧѓГіжБЯпMDЕФБэДяЪНЮЊЃКyЃН2mxЉm2ЃЌШЛКѓгЩжаЕузјБъЙЋЪННсКЯЕуNЁЂEЕФзјБъЃЌБэЪОГіЕуDЕФзјБъЃЌдйНЋЕуDЕФзјБъДњШыжБЯпMDЕФБэДяЪНећРэЧѓНтМДПЩЃЎ
ЃЈ1ЃЉХзЮяЯпC2ЃКyЃНx2ЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНC1ЃК
ЙЪХзЮяЯпC1ЕФНтЮіЪНЮЊЃКyЃНЃЈxЉ1ЃЉ2Љ4ЃЛ
ЃЈ2ЃЉЙ§ЕуBзїyжсЕФЦНааЯпMNЃЌЙ§ЕуCзїCMЁЭMNгкЕуMЃЌЙ§ЕуPзїPNЁЭMNгкЕуNЃЌ
ЁпЁЯPBN+ЁЯBPNЃН90ЁуЃЌЁЯPBN+ЁЯCBMЃН90ЁуЃЌ
ЁрЁЯBCMЃНЁЯPBNЃЌ
ЕБy=0ЪБЃЌМДЃЈxЉ1ЃЉ2Љ4ЃН0ЃЌ
НтЕУЃКx=3Лђx=Ѓ1ЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЌ
ЕБx=2ЪБЃЌyЃНЃЈxЉ1ЃЉ2Љ4ЃНЉ3ЃЌ
ЁрЕуPЕФзјБъЮЊЃКЃЈ2ЃЌЉ3ЃЉЃЌдђNBЃН3ЃЌPNЃН1ЃЌ
ЁрtanЁЯMCBЃНtanЁЯPBNЃН![]() ЃЌ
ЃЌ
ЩшBMЃНmЃЌдђCMЃН3mЃЌдђЕуCЃЈ3Љ3mЃЌmЃЉЃЌ
НЋЕуCЕФзјБъДњШыC1ЕФНтЮіЪНПЩЕУЃКmЃНЃЈ3Љ3mЉ1ЃЉ2Љ4
НтЕУЃКmЃН![]() Лђm=0ЃЈЩсШЅЃЉЃЌДЫЪБ3Љ3mЃН
Лђm=0ЃЈЩсШЅЃЉЃЌДЫЪБ3Љ3mЃН![]() ЃЌ
ЃЌ
ЙЪЕуCЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
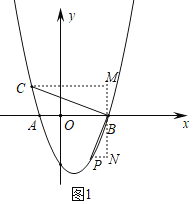
ЃЈ3ЃЉЁпЕуMЁЂNЕФКсзјБъЗжБ№ЮЊmЁЂnЃЌ
ЁрЕуMЁЂNЕФзјБъЮЊЃКЃЈmЃЌm2ЃЉЁЂЃЈnЃЌn2ЃЉЃЌдђЕуEЃЈЉmЃЌm2ЃЉЃЌ
ЩшжБЯпMDЕФБэДяЪНЮЊyЃНkx+bЃЌ
НЋЕуMЕФзјБъДњШыЕУm2=km+bЃЌдђb=m2ЃkmЃЌ
ЁржБЯпMDЕФБэДяЪНЮЊЃКyЃНkx+m2ЉkmЃЌ
СЊСЂyЃНkx+m2ЉkmгыyЃНx2ПЩЕУЃКx2ЃНkx+m2ЉkmЃЌећРэЕУЃКx2ЃkxЃm2ЃЋkmЃН0ЃЌ
ЁпжБЯпMDгыХзЮяЯпC2жЛгавЛИіЙЋЙВЕуЃЌ
ЁрЁїЃНЃЈЃkЃЉ2Љ4ЃЈЉm2+kmЃЉЃНk2+4m2Ѓ4kmЃН0ЃЌ
НтЕУЃКkЃН2mЃЌ
ЙЪжБЯпMDЕФБэДяЪНЮЊЃКyЃН2mxЉm2ЃЌ
ЁпNЃЈnЃЌn2ЃЉЃЌEЃЈЉmЃЌm2ЃЉЃЌ
ИљОнжаЕуЙЋЪНЕУЃКЕуDКсзјБъЮЊЃКЃ2mЃnЃЌЕуDзнзјБъЮЊЃК2m2Љn2ЃЌ
ЁрDЃЈЉ2mЉnЃЌ2m2Љn2ЃЉЃЌ
НЋЕуDЕФзјБъДњШыyЃН2mxЉm2ПЩЕУ2m2Љn2ЃН2m(Љ2mЉn) Љm2ЃЌ
ећРэЕУЃКn2Љ2mnЉ7m2ЃН0ЃЌ
ЗНГЬСНБпЭЌЪБГ§вдm2ЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрnЃН![]() ЃЎ
ЃЎ