题目内容
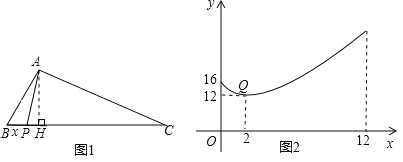
【题目】如图1,在△ABC中,点P为BC边上一点,设BP=x,AP2=y,已知y是x的二次函数的一部分,其图象如图2,点Q(2,12)是图象上的最低点,且图象与y轴交于(0,16).
(1)求y关于x的函数解析式;
(2)当△ABP为直角三角形时,BP的值是多少?
【答案】(1)y=x2﹣4x+16(0≤x≤12);(2)当△ABP为直角三角形时,BP的值是2或8.
【解析】
(1)根据二次函数的顶点式设出抛物线解析式,再将点(0,16)代入即可得出结论;
(2)先根据图2,判断出AB=4,BH=2,BC=12,进而求出∠B=60°,再分两种情况,利用含30度角的直角三角形的性质即可得出结论.
解:(1)∵y是x的二次函数的一部分点,且Q(2,12)是图象上的最低点,
∴y=a(x﹣2)2+12,
∵图象与y轴交于(0,16),
∴a×22+12=16,
∴a=1,
∴y关于x的函数解析式为y=(x﹣2)2+12=x2﹣4x+16(0≤x≤12),
(2)如图1,过点A作AH⊥BC于H,
由图2知,BC=12,BH=2,AB2=16,
∴AB=4,
在Rt△ABH中,cosB=![]() ,
,
∴∠B=60°,
当△ABP为直角三角形时,
①当∠APB=90°时,点P与点H重合,此时,BP=BH=2;
②当∠BAP=90°时,∠APB=90°﹣∠B=30°,
∴BP=2AB=8,
即:当△ABP为直角三角形时,BP的值是2或8.

练习册系列答案
相关题目