Question

【题目】如图，在平面直角坐标系xOy中，ABCO的顶点A，B坐标分别是（6，0），（0，4）．动点P在直线OD解析式为y＝x上运动．

（1）若反比例函数y＝图象过C点，则m＝_____．

（2）证明：OD⊥AB；

（3）当以点P为圆心、PB长为半径的⊙P随点P运动⊙P与ABCO的边所在直线相切时，请直接写出点P的坐标．

Answer 1

【答案】（1）﹣24；（2）见解析；（3）满足条件的P的坐标为（0，0）或（，2）或（6﹣2，9﹣3）．

【解析】

（1）先求出C点的坐标，根据反比例函数y＝图象过C点，代入即可解得m的值；

（2）先求出D点的坐标，D（，），根据OD2+BD2＝OB2，构建直角三角形的三边满足勾股定理，可得OD⊥AB；

（3）本问分4种情况进行讨论，分别是①当⊙P与BC相切时；②当⊙P与OC相切时；③当⊙P与OA相切时；④当⊙P与AB相切时，可根据这4种情况求出点P的坐标.

（1）解：∵A（6，0），B（0，4），

∴OA＝6，OB＝4，

∵四边形OABC是平行四边形，

∴BC＝OA＝6，

∴C（﹣6，4）．

∵反比例函数y＝图象过C点，

∴m＝﹣24，

故答案为﹣24．

（2）证明：∵A（6，0），B（0，4），

∴直线AB的解析式为y＝﹣x+4，

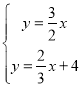由解得，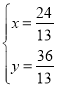

∴D（，），

∴BD2＝（）2+（4﹣）2＝，OD2＝（）2+（）2＝，

∵OD2+BD2＝＝16＝OB2，

∴∠ODB＝90°，

∴OD⊥AB．

（3）解：∵OP⊥AB，AB∥OC

∴OP⊥OC，设P（x，x）

①当⊙P与BC相切时，∵动点P在直线y＝x上，

∴P与O重合，此时圆心P到BC的距离为OB，

∴P（0，0）．

②如图1中，当⊙P与OC相切时，则OP＝BP，△OPB是等腰三角形，作PE⊥y轴于E，则EB＝EO，易知P的纵坐标为2，可得P（，2）．

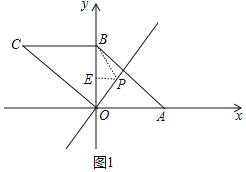
③如图2中，当⊙P与OA相切时，则点P到点B的距离与点P到x轴的距离相等，可得，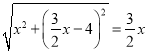

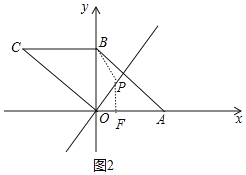
解得x＝6+2或6﹣2，

∵x＝6＝2＞OA，

∴⊙P不会与OA相切，

∴x＝6＝2不合题意，

∴P（6﹣2，9﹣3）．

④如图3中，当⊙P与AB相切时，设线段AB与直线OP的交点为G，此时PB＝PG，

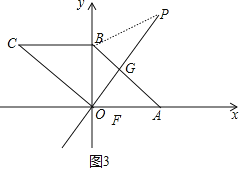
∵OP⊥AB，

∴∠BGP＝∠PBG＝90°不成立，

∴此种情形，不存在P．

综上所述，满足条件的P的坐标为（0，0）或（，2）或（6﹣2，9﹣3）．