题目内容
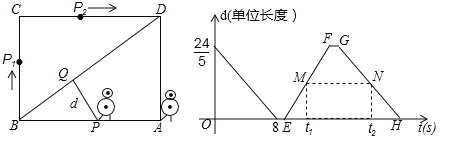
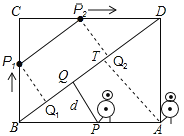
【题目】(2017江苏省苏州市)某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知机器人的速度为1个单位长度/s,移动至拐角处调整方向需要1s(即在B、C处拐弯时分别用时1s).设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段 PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)求AB、BC的长;
(2)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.
【答案】(1)AB=8,BC=6;(2)t1=12,t2=20.
【解析】试题分析:(1)作AT⊥BD,垂足为T,由题意得到AB,AT的长,在Rt△ABT中,根据勾股定理得到BT的长,根据三角函数的定义即可得到结论;
(2)如图,连接P1P2.过P1,P2分别作BD的垂线,垂足为Q1,Q2.则P1Q1∥P2Q2.根据平行线的性质得到d1=d2,得到P1Q1=P2Q2.根据平行线分线段成比例定理得到![]() .设M,N的横坐标分别为t1,t2,于是得到结论.
.设M,N的横坐标分别为t1,t2,于是得到结论.
试题解析:(1)作AT⊥BD,垂足为T,由题意得,AB=8,AT=![]() ,在Rt△ABT中,AB2=BT2+AT2,∴BT=
,在Rt△ABT中,AB2=BT2+AT2,∴BT=![]() ,∵tan∠ABD=
,∵tan∠ABD=![]() ,∴AD=6,即BC=6;
,∴AD=6,即BC=6;
(2)在图①中,连接P1P2.过P1,P2分别作BD的垂线,垂足为Q1,Q2.
则P1Q1∥P2Q2.
∵在图②中,线段MN平行于横轴,∴d1=d2,即P1Q1=P2Q2.∴
P1P2∥BD,∴ ![]() .即
.即![]() .
.
又∵CP1+CP2=7,∴CP1=3,CP2=4.
设M,N的横坐标分别为t1,t2,由题意得,CP1=15﹣t1,CP2=t2﹣16,∴t1=12,t2=20.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?