题目内容
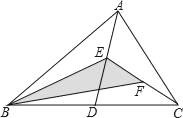
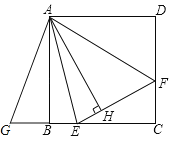
【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为______.
【答案】6.
【解析】
由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中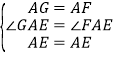 ,
,
∴△GAE≌△FAE.
∵AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x﹣2,FC=x﹣3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x﹣2)2+(x﹣3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.

练习册系列答案
相关题目