题目内容
【题目】
已知:等边三角形ABC
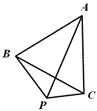
(1)如图1,P为等边△ABC外一点,且∠BPC=120°.试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
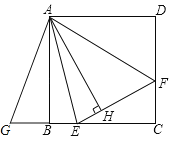
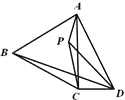
(2)如图2,P为等边△ABC内一点,且∠APD=120°.求证:PA+PD+PC>BD
【答案】(1)猜想:AP=BP+PC,证明见解析;(2)证明见解析.
【解析】
(1)AP=BP+PC,理由是延长BP至E,使PE=PC,连接CE,由∠BPC=120°,推出等边△CPE,得到CP=PE=CE,∠PCE=60°,根据已知等边△ABC,推出AC=BC,∠ACP=∠BCE,根据三角形全等的判定推出△ACP≌△BCE,得出AP=BE即可求出结论;
(2)在AD外侧作等边△AB′D,由(1)得PB′=AP+PD,根据三角形的三边关系定理得到PA+PD+PC>CB′,再证△AB′C≌△ADB,根据全等三角形的性质推出CB′=BD即可.
(1)猜想:AP=BP+PC,
证明:延长BP至E,使PE=PC,连接CE,
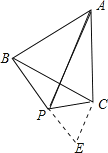
∵∠BPC=120°
∴∠CPE=60°又PE=PC,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°
∴∠ACB=∠PCE
∴∠ACB+∠BCP=∠PCE+∠BCP
∴∠ACP=∠BCE,
∴△ACP≌△BCE(SAS)
∴AP=BE,
∵BE=BO+PE
∴AP=BP+PC
(2)证明:在AD外侧作等边△AB’D,

则点P在三角形AB’D外,连接PB’,B’C,
∵∠APD=120°
∴由(1)得PB’=AP+PD,
在△PB’C中,有PB’+PC’>CB’,
∴PA+PB+PC>CB’,
∵△AB’D、△ABC是等边三角形,
∴AC=AB,AB’=AD
∠BAD=∠CAB’
∴△AB’C≌△ADB
∴CB’=BD,
∴PA+PD+PC>BD.