ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§![]() ΈΣ
ΈΣ![]() ÷αΗΚΑκ÷α…œΒΡΒψΘ§
÷αΗΚΑκ÷α…œΒΡΒψΘ§![]() ΈΣ
ΈΣ![]() ÷αΗΚΑκ÷α…œΒΡΒψ.
÷αΗΚΑκ÷α…œΒΡΒψ.
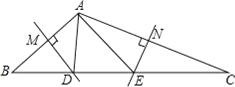
(1)»γΆΦ1Θ§“‘![]() ΒψΈΣΕΞΒψΓΔ
ΒψΈΣΕΞΒψΓΔ![]() ΈΣ―ϋ‘ΎΒΎ»ΐœσœόΉςΒ»―ϋ
ΈΣ―ϋ‘ΎΒΎ»ΐœσœόΉςΒ»―ϋ![]() Θ§»τ
Θ§»τ![]() Θ§
Θ§![]() Θ§ ‘«σ
Θ§ ‘«σ![]() ΒψΒΡΉχ±ξΘΜ
ΒψΒΡΉχ±ξΘΜ
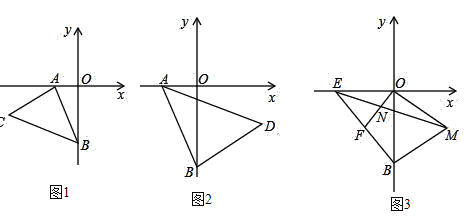
(2)»γΆΦ![]() Θ§»τΒψ
Θ§»τΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉίΉχ±ξΈΣ
ΒΡΉίΉχ±ξΈΣ![]() Θ§“‘
Θ§“‘![]() ΈΣΕΞΒψΘ§
ΈΣΕΞΒψΘ§![]() ΈΣ―ϋΉςΒ»―ϋ
ΈΣ―ϋΉςΒ»―ϋ![]() . ‘Έ ΘΚΒ±
. ‘Έ ΘΚΒ±![]() Βψ―Ί
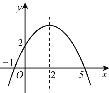
Βψ―Ί![]() ÷αΗΚΑκ÷αœρœ¬‘ΥΕ·«“ΤδΥϊΧθΦΰΕΦ≤Μ±δ ±Θ§’ϊ Ϋ
÷αΗΚΑκ÷αœρœ¬‘ΥΕ·«“ΤδΥϊΧθΦΰΕΦ≤Μ±δ ±Θ§’ϊ Ϋ![]() ΒΡ÷Β «ΖώΖΔ…ζ±δΜ·ΘΩ»τ≤ΜΖΔ…ζ±δΜ·Θ§«κ«σ≥ωΤδ÷ΒΘΜ»τΖΔ…ζ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ
ΒΡ÷Β «ΖώΖΔ…ζ±δΜ·ΘΩ»τ≤ΜΖΔ…ζ±δΜ·Θ§«κ«σ≥ωΤδ÷ΒΘΜ»τΖΔ…ζ±δΜ·Θ§«κΥΒΟςάμ”…ΘΜ
(3)»γΆΦ![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ÷αΗΚΑκ÷α…œΒΡ“ΜΒψΘ§«“
÷αΗΚΑκ÷α…œΒΡ“ΜΒψΘ§«“![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§“‘
Θ§“‘![]() ΈΣ±ΏΉςΒ»±Ώ
ΈΣ±ΏΉςΒ»±Ώ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ ‘ΧΫΥςΘΚ‘ΎœΏΕΈ
Θ§ ‘ΧΫΥςΘΚ‘ΎœΏΕΈ![]() ΓΔ
ΓΔ![]() ΚΆ
ΚΆ![]() ÷–Θ§ΡΡΧθœΏΕΈΒ»”Ύ
÷–Θ§ΡΡΧθœΏΕΈΒ»”Ύ![]() ”κ
”κ![]() ΒΡ≤νΒΡ“ΜΑκΘΩ«κΡψ–¥≥ω’βΗωΒ»ΝΩΙΊœΒΘ§≤ΔΦ”“‘÷ΛΟς.
ΒΡ≤νΒΡ“ΜΑκΘΩ«κΡψ–¥≥ω’βΗωΒ»ΝΩΙΊœΒΘ§≤ΔΦ”“‘÷ΛΟς.
ΓΨ¥πΑΗΓΩ(1) C(-6,-2);(2)≤ΜΖΔ…ζ±δΜ·Θ§÷ΒΈΣ![]() ΘΜΘ®3Θ©EN=
ΘΜΘ®3Θ©EN=![]() (EM-ON)Θ§÷ΛΟςΦϊœξΫβ.
(EM-ON)Θ§÷ΛΟςΦϊœξΫβ.
ΓΨΫβΈωΓΩ
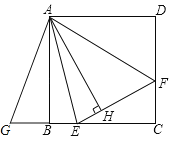
Θ®1Θ©ΉςCQΓΆOA”ΎΒψQ,Ω…“‘÷ΛΟς![]() Θ§”…QC=AD,AQ=BO,‘Ό”…ΧθΦΰΨΆΩ…“‘«σ≥ωΒψCΒΡΉχ±ξΘΜ
Θ§”…QC=AD,AQ=BO,‘Ό”…ΧθΦΰΨΆΩ…“‘«σ≥ωΒψCΒΡΉχ±ξΘΜ
Θ®2Θ©ΉςDPΓΆOB”ΎΒψPΘ§Ω…“‘÷ΛΟς![]() Θ§‘ρ”–BP=OB-PO=m-(-n)=m+nΈΣΕ®÷ΒΘ§¥”ΕχΩ…“‘«σ≥ωΫα¬έ
Θ§‘ρ”–BP=OB-PO=m-(-n)=m+nΈΣΕ®÷ΒΘ§¥”ΕχΩ…“‘«σ≥ωΫα¬έ![]() ΒΡ÷Β≤Μ±δΈΣ
ΒΡ÷Β≤Μ±δΈΣ![]() .
.
Θ®3Θ©ΉςBHΓΆEB”ΎΒψBΘ§”…ΧθΦΰΩ…“‘ΒΟ≥ωΓœ1=30Γψ,Γœ2=Γœ3=ΓœEMO=15Γψ,ΓœEOF=ΓœBMG=45Γψ,EO=BM,Ω…“‘÷ΛΟς![]() Θ§‘ρGM=ON,ΨΆ”–EM-ON=EM-GM=EG,ΉνΚσ”…ΤΫ––œΏΖ÷œΏΕΈ≥…±»άΐΕ®άμΨΆΩ…ΒΟ≥ωEN=
Θ§‘ρGM=ON,ΨΆ”–EM-ON=EM-GM=EG,ΉνΚσ”…ΤΫ––œΏΖ÷œΏΕΈ≥…±»άΐΕ®άμΨΆΩ…ΒΟ≥ωEN=![]() (EM-ON).
(EM-ON).
Θ®1Θ©»γΆΦΘ®1Θ©ΉςCQΓΆOA”ΎQ,
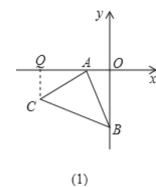
ΓύΓœAQC=90Γψ,
ΓΏ![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύAC=AB,ΓœCAB=90Γψ,
ΓύΓœQAC+ΓœOAB=90Γψ,
ΓΏΓœQAC+ΓœACQ=90Γψ,
ΓύΓœACQ=ΓœBAO,
”÷ΓΏAC=AB,ΓœAQC=ΓœAOB,
Γύ![]() (AAS),
(AAS),
ΓύCQ=AO,AQ=BO,
ΓΏOA=2,OB=4,
ΓύCQ=2,AQ=4,
ΓύOQ=6,
ΓύC(-6,-2).
(2)»γΆΦΘ®2Θ©ΉςDPΓΆOB”ΎΒψP,
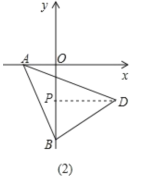
ΓύΓœBPD=90Γψ,
ΓΏ![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύAB=BD,ΓœABD=ΓœABO+ΓœOBD=90Γψ,
ΓΏΓœOBD+ΓœBDP=90Γψ,
ΓύΓœABO=ΓœBDP,
”÷ΓΏAB=BD,ΓœAOB=ΓœBPD=90Γψ,
Γύ![]()
ΓύAO=BP,
ΓΏBP=OB-PO=m-(-n)=m+n,
ΓΏA![]() ,
,
ΓύOA=![]() ,
,
Γύm+n=![]() ,
,
ΓύΒ±ΒψB―Ίy÷αΗΚΑκ÷αœρœ¬‘ΥΕ· ±Θ§AO=BP=m+n=![]() ,
,
Γύ’ϊ Ϋ![]() ΒΡ÷Β≤Μ±δΈΣ
ΒΡ÷Β≤Μ±δΈΣ![]() .
.
Θ®3Θ©![]()
÷ΛΟςΘΚ»γΆΦΘ®3Θ©Υυ ΨΘ§‘ΎME…œ»Γ“ΜΒψG ΙΒΟMG=ON,Ν§Ϋ”BG≤Δ―”≥ΛΘ§ΫΜx÷α”ΎH.
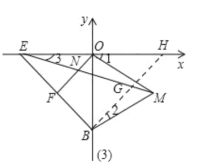
ΓΏ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύBO=BM=MO,ΓœOBM=ΓœOMB=ΓœBOM=60Γψ,
ΓύEO=MO,ΓœEBM=105Γψ,Γœ1=30Γψ,
ΓΏOE=OB,
ΓύOE=OM=BM,
ΓύΓœ3=ΓœEMO=15Γψ,
ΓύΓœBEM=30Γψ,ΓœBME=45Γψ,
ΓΏOFΓΆEB,
ΓύΓœEOF=ΓœBME,
Γύ![]() ,
,
ΓύBG=EN,
ΓΏON=MG,
ΓύΓœ2=Γœ3,
ΓύΓœ2=15Γψ,
ΓύΓœEBG=90Γψ,
ΓύBG=![]() EG,
EG,
ΓύEN=![]() EG,
EG,
ΓΏEG=EM-GM,
ΓύEN=![]() (EM-GM),
(EM-GM),
ΓύEN=![]() (EM-ON).
(EM-ON).

 ΧλΧλΝΖΩΎΥψœΒΝ–¥πΑΗ
ΧλΧλΝΖΩΎΥψœΒΝ–¥πΑΗ