题目内容
【题目】如图,正方形![]() 的对角线
的对角线![]() 和
和![]() 相交于点
相交于点![]() ,正方形
,正方形![]() 的边
的边![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
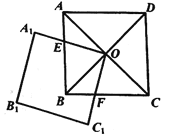
(1)求证:![]() ;
;
(2)如果正方形![]() 的边长为
的边长为![]() ,那么正方形
,那么正方形![]() 绕
绕![]() 点转动的过程中,与正方形
点转动的过程中,与正方形![]() 重叠部分的面积始终等于__________.(用含
重叠部分的面积始终等于__________.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)见解析;(2)![]()
【解析】
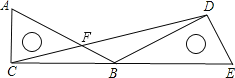
(1)由题意得OA=OB,∠OAB=∠OBC=45°又因为∠AOE+∠EOB=90°,∠BOF+∠EOB=90°可得∠AOE=∠BOF,根据ASA可证△AOE≌△BOF,可得AE=BF,可得BE+BF=AB,由勾股定理可得结论;
(2)由全等三角形的性质可得S△AOE=S△BOF,可得重叠部分的面积为正方形面积的![]() ,即可求解.
,即可求解.
(1)在正方形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
则![]() ,
,
∵正方形![]() 中
中![]() ,
,
∴![]() ,∴
,∴![]() .
.
在![]() 和
和![]() 中,
中,
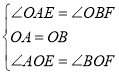 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵△AOE≌△BOF,
∴S△AOE=S△BOF,
∴重叠部分的面积=S△AOB=![]() S正方形ABCD=
S正方形ABCD=![]() ,
,
故答案为:![]()

练习册系列答案
相关题目