题目内容
【题目】已知抛物线 ![]() :y=ax2 过点(2,2)
:y=ax2 过点(2,2)
(1)直接写出抛物线的解析式;
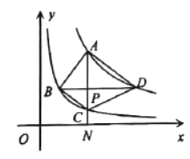
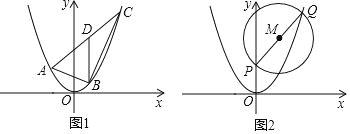
(2)如图,△ABC 的三个顶点都在抛物线![]() 上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求
上,且边 AC 所在的直线解析式为y=x+b,若 AC 边上的中线 BD 平行于 y 轴,求![]() 的值;
的值;
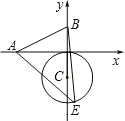
(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上![]() 上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
上一动点,以 PQ 为直径作⊙M,直线 y=t 与⊙M 相交于 H、K 两点是否存在实数 t,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)16;(3)见解析.
;(2)16;(3)见解析.
【解析】
(1)把点(2,2)坐标代入 y=ax2 即可求解;
(2)把 y=x+b 和 y=![]() x2 得:x2﹣2x﹣2b=0,设 A、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1x2=﹣2b,可以求出点 D坐标、B坐标,即可求解;;
x2 得:x2﹣2x﹣2b=0,设 A、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1x2=﹣2b,可以求出点 D坐标、B坐标,即可求解;;
(3)设点 Q坐标为(a,![]() a2),点 M的坐标为(
a2),点 M的坐标为(![]() ,
,![]() a2+1),圆的半径为 r,则 r2=
a2+1),圆的半径为 r,则 r2=![]() +(
+(![]() a2﹣1)2=
a2﹣1)2=![]() a4﹣
a4﹣![]() a2+1,点 M 到直线 y=t 的距离为 d, 用 HK=2
a2+1,点 M 到直线 y=t 的距离为 d, 用 HK=2![]() =2
=2![]() ,当
,当![]() =0时,HK为常数,t=
=0时,HK为常数,t=![]() ,HK=
,HK=![]() .
.
(1)把点(2,2)坐标代入y=ax2,解得:a=![]() ,
,
∴抛物线的解析式为y=x2;
(2)把y=x+b和y=![]() x2得:x2﹣2x﹣2b=0,
x2得:x2﹣2x﹣2b=0,
设A、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1x2=﹣2b,
点D坐标为(![]() ,
,![]() ),即D(1,﹣b),B坐标为(1,
),即D(1,﹣b),B坐标为(1,![]() ),
),
AC2=[![]() (x2﹣x1)]2=16b+8,
(x2﹣x1)]2=16b+8,
BD=![]() +b,
+b,
∴![]() =16;
=16;
(3)设点Q坐标为(a,![]() a2),
a2),
点P的坐标为(0,2),由 P、Q坐标得点M的坐标为(![]() ,
,![]() a2+1),
a2+1),
设圆的半径为 r,由P(0,2)、M 两点坐标可得r2=![]() +(
+(![]() a2﹣1)2=
a2﹣1)2=![]() a4﹣
a4﹣![]() a2+1,
a2+1,
设点M到直线y=t的距离为d,则d2=(a2+1﹣t)=![]() a4+
a4+![]() a2+1+t2﹣2t﹣
a2+1+t2﹣2t﹣![]() a2t,
a2t,
则 HK=2![]() =2
=2![]() ,
,
当![]() =0 时,HK为常数,t=
=0 时,HK为常数,t=![]() ,
,
HK=![]() .
.