题目内容
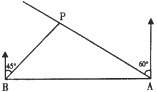
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
【答案】(1)6+6![]() (2)3+3
(2)3+3![]()
【解析】
(1)过点P作PD⊥AB于点D,先解Rt△PBD,得到BD和PD的长,再解Rt△PAD,得到AD和AP的长,然后根据BD+AD=AB,即可求解; (2)过点B作BF⊥AC于点F,解直角三角形即可得到结论.
(1)如图,过点P作PD⊥AB于点D.
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=6km.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=![]() PD=6
PD=6![]() km,PA=12.
km,PA=12.
∴AB=BD+AD=(6+6![]() )km;
)km;
(2)如图,过点B作BF⊥AC于点F,
则∠BAP=30°,
∵AB=(6+6![]() ),
),
∴BF=![]() AB=(3+3
AB=(3+3![]() )km.
)km.
∴观测站B到射线AP的最短距离为(3+3![]() )km.
)km.

练习册系列答案
相关题目