题目内容
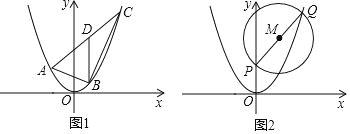
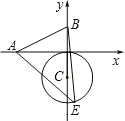
【题目】如图,已知 A、B 两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为 1,E 是⊙C 上的一动点,则△ABE 面积的最大值为( )
A. ![]() B. 3+
B. 3+![]() C. 3+
C. 3+![]() D. 4+
D. 4+![]()
【答案】A
【解析】
过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值,点E在过点C垂直于AB的直线和圆C在点C下方的交点,然后求出直线AB解析式,进而得出CD解析式,即可得出点D坐标,再求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
如图,过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大即可),
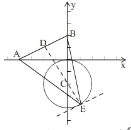
设直线AB的解析式为y=kx+b(k≠0),
∵A(﹣2,0),B(0,1),
∴![]() ,
,
解得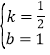 ,
,
∴直线AB的解析式为 y=![]() x+1 ①,
x+1 ①,
∵CD⊥AB,C(0,﹣1),
∴直线CD的解析式为y=﹣2x﹣1 ②,
联立①②得,D(﹣![]() ,
,![]() ),
),
∴CD=![]() =
=![]() ,
,
∵⊙C的半径为1,
∴DE=CD+CE=![]() +1,
+1,
∵A(﹣2,0),B(0,1),
∴AB=![]() ,
,
∴S△ABE的最大值=![]() ABDE=
ABDE=![]() (
(![]() +1)×
+1)×![]() =2+
=2+![]() .
.
故选 A.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

【题目】如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形,……
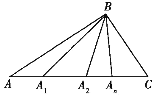
(1)完成下表:
连接个数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现三角形个数 | 3 | 6 |
(2)若出现了45个三角形,则共连接了_____个点?若一直连接到An,则图中共有______个三角形.