题目内容
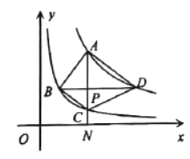
【题目】如图,四边形![]() 在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数
在平面直角坐标系的第一象限内,其四个顶点分别在反比例函数![]() 与
与![]() 的图象上,对角线
的图象上,对角线![]() 于点
于点![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)若![]() ,试求
,试求![]() 的值;
的值;
(2)当![]() ,点
,点![]() 是线段
是线段![]() 的中点时,试判断四边形
的中点时,试判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
(3)直线![]() 与
与![]() 轴相交于
轴相交于![]() 点.当四边形
点.当四边形![]() 为正方形时,请求出
为正方形时,请求出![]() 的长度.
的长度.
【答案】(1)1;(2)(2)四边形ABCD为菱形,理由见解析;(3)![]()
【解析】
(1)由点N的坐标及CN的长度可得出点C的坐标,再利用反比例函数图象上点的坐标特征可求出点n的值;
(2)利用反比例函数图象上点的坐标特征可得出点A,C的坐标,结合点P为线段AC的中点可得出点P的坐标,利用反比例函数图象上点的坐标特征可得出点B,D的坐标,结合点P的坐标可得出BP=DP,利用“对角线互相垂直平分的四边形为菱形”可证出四边形ABCD为菱形;
(3)利用正方形的性质可得出AC=BD且点P为线段AC及BD的中点,利用反比例函数图象上点的坐标特征可求出点A,C,B,D的坐标,结合AC=BD可得出关于n的方程,解之即可得出结论.
(1)∵点N的坐标为(2,0),CN⊥x轴,且![]() ,
,
∴点C的坐标为(2,![]() ).
).
∵点C在反比例函数![]() 的图象上,
的图象上,
∴n=2×![]() =1.
=1.
(2)四边形ABCD为菱形,理由如下:
当n=2时,![]() .
.
当x=2时,![]() ,
,
∴点C的坐标为(2,1),点A的坐标为(2,4).
∵点P是线段AC的中点,
∴点P的坐标为(2,![]() ).
).
当y=![]() 时,
时,![]() ,
,
解得:![]() ,
,
∴点B的坐标为![]() ,点D的坐标为
,点D的坐标为![]() ,
,
∴![]() ,
,
∴BP=DP.
又∵AP=CP,AC⊥BD,
∴四边形ABCD为菱形.
(3)∵四边形ABCD为正方形,
∴AC=BD,且点P为线段AC及BD的中点.
当x=2时,y1=![]() n,y2=2n,
n,y2=2n,
∴点A的坐标为(2,2n),点C的坐标为(2,![]() n),AC=
n),AC=![]() n,
n,
∴点P的坐标为![]() .
.
同理,点B的坐标为![]() ,点D的坐标为
,点D的坐标为![]() ,
,![]() .
.
∵AC=BD,
∴![]() ,
,
∴![]() ,
,
∴点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() .
.
设直线AB的解析式为y=kx+b(k≠0),
将A![]() ,B
,B![]() 代入y=kx+b,得:
代入y=kx+b,得: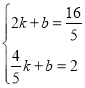 ,
,
解得:![]() ,
,
∴直线AB的解析式为y=x+![]() .
.
当x=0时,y=x+![]() ,
,
∴点E的坐标为(0,![]() ),
),
∴当四边形ABCD为正方形时,OE的长度为![]() .
.

【题目】某公司计划组织员工外出甲、乙旅行社的服务质量相问,且对外报价都是300元/人,该公司联系时,甲旅行社表示可给每人八折优惠;乙旅行社表示可免去一人的费用,其余人九折优惠.
(1)根据题意,填写下表:
外出人数(人) | 10 | 11 |
甲旅行社收费(元) | ____ | 2640 |
乙旅行社收费(元) | 2430 | ____ |
(2)设该公司此次外出有![]() 人,选择甲旅行社的费用为
人,选择甲旅行社的费用为![]() 元,选择乙旅行社的费用为
元,选择乙旅行社的费用为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式
的函数关系式
(3)该公司外出人数在什么范围内,选甲旅行社划算?