Question

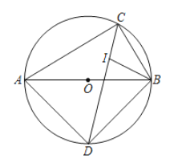
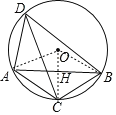
【题目】如图，AB是⊙O的一条弦，C、D是⊙O上的两个动点，且在AB弦的异侧，连接CD．

（1）若AC=BC，AB平分∠CBD，求证：AB=CD；

（2）若∠ADB=60°，⊙O的半径为1，求四边形ACBD的面积最大值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）证=＝即可得=，继而求证结论；

（2）如图,连接OA、OB、OC，OC交AB于H，由∠ADB=60°和AC=BC 求得∠ADC=∠BDC= =30°，OC⊥AB，AH=BH ，继而求出AB的长，由S四边形ABCD＝S△ABD+ S△ABC可知，当D点为优弧AB的中点时，即CD为⊙O的直径时，四边形ACBD的面积最大，进而求解．

（1）∵AC=BC，

∴=

∵AB平分∠CBD，

∴∠ABC=∠ABD，

∴=，

∴=，

∴AB=CD；

（2）连接OA、OB、OC，OC交AB于H，如图，

∵=，

∴∠ADC=∠BDC=∠ADB=30°，OC⊥AB，AH=BH，

∴∠BOC=60°，

∴OH= OB=，BH= OH=，

∴AB=2BH=．

∵四边形ACBD的面积=S△ABC+S△ABD，

∴当D点到AB的距离最大时，S△ABD的面积最大，四边形ACBD的面积最大，此时D点为优弧AB的中点，

即CD为⊙O的直径时，四边形ACBD的面积最大，

∴四边形ACBD的面积最大值为 ×2=．