��Ŀ����
����Ŀ��������ABCD�ı߳�Ϊ3����E��F�ֱ�������DC��DA���˶�����DE=DF������BF����EH��BF����ֱ���ڵ�H������CH��
��1����ͼ1������E��DC���е㣬CH��AB֮���������ϵ�� ��
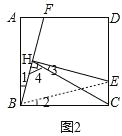
��2����ͼ2������E��DC�����Ҳ���DC���е�ʱ����1���еĽ����Ƿ����������������֤��������������˵�����ɣ�
��3����ͼ3������E��F�ֱ�������DC��DA���˶�ʱ������DH������D��ֱ��DH�Ĵ��ߣ���ֱ��BF�ڵ�K������CK����ֱ��д���߶�CK�������ֵ��
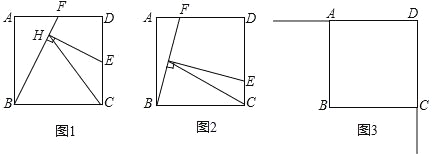
���𰸡���1��CH=AB����2������E��DC�����Ҳ���DC���е�ʱ����1���еĽ���CH=AB��Ȼ������֤��������.��3��![]() ��
��
��������
�����������1�����ȸ���ȫ���������ж��ķ������жϳ���ABF�ա�CBE�������жϳ���1=��2��Ȼ�����EH��BF����BCE=90�㣬�ɵ�C��H���㶼����BEΪֱ����Բ�ϣ��жϳ���4=��HBC�������жϳ�CH=BC��������AB=BC���жϳ�CH=AB���ɣ�
��2�����ȸ���ȫ���������ж��ķ������жϳ���ABF�ա�CBE�������жϳ���1=��2��Ȼ�����EH��BF����BCE=90�㣬�ɵ�C��H���㶼����BEΪֱ����Բ�ϣ��жϳ���4=��HBC�������жϳ�CH=BC��������AB=BC���жϳ�CH=AB���ɣ�
��3�����ȸ������������ߵĹ�ϵ���ɵ�CK��AC+AK���ݴ��жϳ���C��A��K���㹲��ʱ��CK�ij����Ȼ�����ȫ���������ж��ķ������жϳ���DFK�ա�DEH�������жϳ�DK=DH���ٸ���ȫ���������ж��ķ������жϳ���DAK�ա�DCH�������жϳ�AK=CH=AB��������CK=AC+AK=AC+AB������߶�CK�������ֵ�Ƕ��ټ��ɣ�
�����������1����ͼ1������BE��
 ��
��
��������ABCD��
AB=BC=CD=AD����A=��BCD=��ABC=90�㣬
�ߵ�E��DC���е㣬DE=DF��
���F��AD���е㣬
��AF=CE��
�ڡ�ABF�͡�CBE�У�

���ABF�ա�CBE��
���1=��2��
��EH��BF����BCE=90�㣬
��C��H���㶼����BEΪֱ����Բ�ϣ�
���3=��2��
���1=��3��
�ߡ�3+��4=90�㣬��1+��HBC=90�㣬
���4=��HBC��
��CH=BC��
�֡�AB=BC��
��CH=AB��
��2������E��DC�����Ҳ���DC���е�ʱ����1���еĽ���CH=AB��Ȼ������
��ͼ2������BE��
 ��
��
��������ABCD��
AB=BC=CD=AD����A=��BCD=��ABC=90�㣬
��AD=CD��DE=DF��
��AF=CE��
�ڡ�ABF�͡�CBE�У�

���ABF�ա�CBE��
���1=��2��
��EH��BF����BCE=90�㣬
��C��H���㶼����BEΪֱ����Բ�ϣ�
���3=��2��
���1=��3��
�ߡ�3+��4=90�㣬��1+��HBC=90�㣬
���4=��HBC��
��CH=BC��
�֡�AB=BC��
��CH=AB��
��3����ͼ3��
 ��
��
��CK��AC+AK��
�൱C��A��K���㹲��ʱ��CK�ij����
�ߡ�KDF+��ADH=90�㣬��HDE+��ADH=90�㣬
���KDF=��HDE��
�ߡ�DEH+��DFH=360��-��ADC-��EHF=360��-90��-90��=180�㣬
��DFK+��DFH=180�㣬
���DFK=��DEH��
�ڡ�DFK�͡�DEH�У�
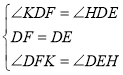
���DFK�ա�DEH��
��DK=DH��
�ڡ�DAK�͡�DCH�У�

���DAK�ա�DCH��
��AK=CH
�֡�CH=AB��
��AK=CH=AB��
��AB=3��
��AK=3��AC=3![]() ��
��
��CK=AC+AK=AC+AB=![]() ��
��
���߶�CK�������ֵ��![]() ��
��