题目内容
【题目】如图,直线x=t与反比例函数y=![]() ,y=﹣
,y=﹣![]() 的图象交于点A,B,直线y=2t与反比例y=
的图象交于点A,B,直线y=2t与反比例y=![]() ,y=﹣
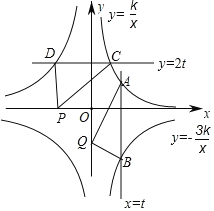
,y=﹣![]() 的图象交于点C,D,其中常数t,k均大于0.点P,Q分别是x轴、y轴上任意点,若S△PCD=S1,S△ABQ=S2.则下列结论正确的是( )
的图象交于点C,D,其中常数t,k均大于0.点P,Q分别是x轴、y轴上任意点,若S△PCD=S1,S△ABQ=S2.则下列结论正确的是( )
A.S1=2tB.S2=4kC.S1=2S2D.S1=S2
【答案】D
【解析】
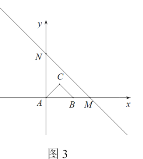
先设AB与x轴的交点为M,CD与y轴的交点为N,连接OA、OB、OC、OD.根据同底等高的三角形面积相等这一性质证得S△ABQ=S△AOB、S△PCD=S△COD,再结合平行于坐标轴的直线上的点的坐标特征求出S△ABQ=S△AOB=2k,S△PCD=S△COD=2k即可解答.
解:设AB与x轴的交点为M,CD与y轴的交点为N,连接OA、OB、OC、OD.
∵直线x=t与反比例函数y=![]() ,y=﹣
,y=﹣![]() 的图象交于点A,B,
的图象交于点A,B,
∴AB∥y轴,
∴S△ABQ=S△AOB.
∵S△AOB=S△AOM+S△BOM,S△AOM=![]() k,S△BOM=
k,S△BOM=![]() ×3k=
×3k=![]() k,
k,
∴S△ABQ=S△AOB=![]() k +
k +![]() k=2k,
k=2k,
同理证得:S△PCD=S△COD=2k,
∴S△PCD=S△ABQ,
∴S1=S2.
故选:D.


练习册系列答案
相关题目