题目内容
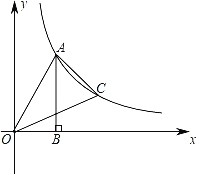
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=
(x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB=![]() .点C是反比例函数y=
.点C是反比例函数y=![]() (x>0)图象上一动点,连接AC,OC,若△AOC的面积为
(x>0)图象上一动点,连接AC,OC,若△AOC的面积为![]() ,则点C的坐标为_____.
,则点C的坐标为_____.
【答案】(4,![]() ).
).
【解析】
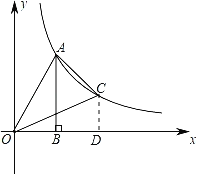
作CD⊥x轴于D,解直角三角形求得A(2,5),设点C的坐标为(m,![]() ),根据S△AOC=S△AOB+S梯形ABDC﹣S△COD=S梯形ABDC,得出
),根据S△AOC=S△AOB+S梯形ABDC﹣S△COD=S梯形ABDC,得出![]() (5+
(5+![]() )(m﹣2)=
)(m﹣2)=![]() ,解得m=4,即可求得C点的坐标.
,解得m=4,即可求得C点的坐标.
解:作CD⊥x轴于D,
∵点A是反比例函数y=![]() (x>0)图象上一点,设A(x,
(x>0)图象上一点,设A(x,![]() ),
),
∴OB=x,AB=![]() ,
,
∵tan∠OAB=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得x=2,
,解得x=2,
∴A(2,5)
设点C的坐标为(m,![]() )
)
∵S△AOC=S△AOB+S梯形ABDC﹣S△COD=S梯形ABDC,△AOC的面积为![]() ,
,
∴![]() (AB+CD)BD=
(AB+CD)BD=![]() ,
,
∴![]() (5+
(5+![]() )(m﹣2)=
)(m﹣2)=![]() ,
,
整理得,m2﹣3m﹣4=0,
解得m=4或m=﹣1(舍去),
∴点C的坐标为(4,![]() ),
),
故答案为(4,![]() ).
).

练习册系列答案
相关题目