题目内容
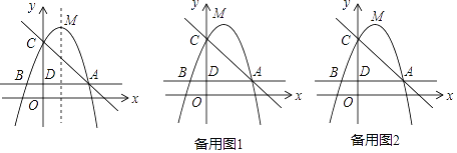
【题目】如图，在平面直角坐标系中，△CDE的顶点C点坐标为C（1，﹣2），点D的横坐标为
，将△CDE绕点C旋转到△CBO，点D的对应点B在x轴的另一个交点为点A．
（1）图中，∠OCE等于∠_____；
（2）求抛物线的解析式；
（3）抛物线上是否存在点P，使S△PAE=
S△CDE？若存在，直接写出点P的坐标；若不存在，请说明理由．
【答案】（1）BCD；（2）y=
x2﹣x﹣
；（3）存在；（1+
，1）或（1﹣，1）或（1+
，﹣1）或（1﹣，1）．
【解析】
（1）根据旋转的性质易得∠OCE=∠BCD；
（2）（2）作CH⊥OE于H，如图，根据旋转的性质得CO=CE，CB=CD，OB=DE，则利用等腰三角形的性质得OH=HE=1，则E点坐标为（2，0），设B（m，0），D（
，n），再利用两点间的距离公式求得m、n的值，然后设顶点式y=a（x-1）2-2，再把B点坐标代入求出a即可得到抛物线解析式；
（3）先利用抛物线的对称性得到A（-1，0），再根据旋转的性质得△CDE≌△CBO，则S△CDE=S△CBO=3，设P（t，t2﹣t﹣），利用三角形面积公式得到关于t的方程，解关于t的一元二次方程求出t，从而可得到满足条件的P点坐标．
解：（1）∵△CDE绕点C旋转到△CBO，
∴∠OCE=∠BCD；
故答案为BCD；
（2）作CH⊥OE于H，如图，
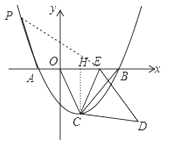
∵△CDE绕点C旋转到△CBO，
∴CO=CE，CB=CD，OB=DE，
∴OH=HE=1，
∴OE=2，
∴E点坐标为（2，0），
设B（m，0），D（，n），
∵CD2=（1﹣）2+（﹣2﹣n）2 ， CB2=（1﹣m）2+22 ， DE2=（2﹣）2+n2 ，
∴（1﹣）2+（﹣2﹣n）2=（1﹣m）2+22 ， （2﹣）2+n2=m2 ，
∴m=3，n=﹣
，
∴B（3，0），
设抛物线解析式为y=a（x﹣1）2﹣2，
把B（3，0）代入得4a﹣2=0，解得a=，
∴抛物线解析式为y=（x﹣1）2﹣2，即y=
x2﹣x﹣；
（3）存在．
A与点B关于直线x=1对称，
∴A（﹣1，0），
∵△CDE绕点C旋转到△CBO，
∴△CDE≌△CBO，
∴S△CDE=S△CBO=23=3，
设P（t，t2﹣t﹣），
∵S△PAE=S△CDE ，
∴3|t2﹣t﹣|=3，
∴t2﹣t﹣=1或t2﹣t﹣=﹣1，
解方程t2﹣t﹣=1得t1=1+，t2=1﹣，此时P点坐标为（1+，1）或（1﹣，1）；
解方程t2﹣t﹣=﹣1得t1=1+，t2=1﹣，此时P点坐标为（1+span>，﹣1）或（1﹣，1）；
综上所述，满足条件的P点坐标为（1+，1）或（1﹣，1）或（1+，﹣1）或（1﹣，1）．
