题目内容
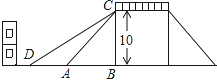
【题目】如图是一座人行天桥的示意图，天桥的高度是10米，CB⊥DB，坡面AC的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC的坡度为i=
：3．若新坡角下需留3米宽的人行道，问离原坡角（A点处）10米的建筑物是否需要拆除？（参考数据： 
≈1.414， 
≈1.732）
【答案】需要拆除．
【解析】试题分析：由题意得到△ABC为等腰直角三角形，求出AB的长，在Rt△BCD中，根据新坡面的坡度求出∠BDC=30°，得到DC的长，再利用勾股定理求出DB的长，由DB﹣AB求出AD的长，再比较AD+3与10的大小即可．
试题解析：需要拆除，理由为：
∵CB⊥AB，∠CAB=45°，∴△ABC为等腰直角三角形，∴AB=BC=10米，在Rt△BCD中，新坡面DC的坡度为i=
：3，即∠CDB=30°，∴DC=2BC=20米，BD=
=
米，∴AD=BD﹣AB=（
）米≈7．32米，∵3+7．32=10．32＞10，∴需要拆除．
练习册系列答案
相关题目
