题目内容
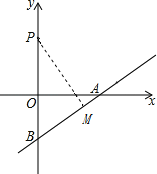
【题目】如图,在平面直角坐标系中,点P的坐标为(0,2),直线y=![]() 与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )
与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为( )

A.3 B.4 C.5 D.6
【答案】B
【解析】
试题分析:根据垂线段最短得出PM⊥AB时线段PM最短,分别求出PB、OB、OA、AB的长度,利用△PBM∽△ABO,即可求出本题的答案.
解:如图,过点P作PM⊥AB,则:∠PMB=90°,当PM⊥AB时,PM最短,
∵直线y=![]() x﹣3与x轴、y轴分别交于点A,B,
x﹣3与x轴、y轴分别交于点A,B,
∴点A的坐标为(4,0),点B的坐标为(0,﹣3),
在Rt△AOB中,AO=4,BO=3,AB=![]() =5,
=5,
∵∠BMP=∠AOB=90°,∠B=∠B,PB=OP+OB=5,
∴△PBM∽△ABO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得:PM=4.
,解得:PM=4.
故选B.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目