题目内容
【题目】叙述并证明三角形内角和定理.
三角形内角和定理： ;
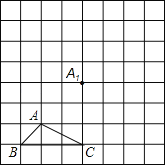
已知：如图△ABC.
求证： .
证明：
【答案】三角形的内角和是180°；∠A+∠B+∠C=180°；证明见解析.
【解析】
要证明三角形的三个内角的和为180°，可以把三角形三个角转移到一个平角上，利用平角的性质解答.
解：定理：三角形的内角和是180°；
已知：如图△ABC；
求证：∠A+∠B+∠C=180°.
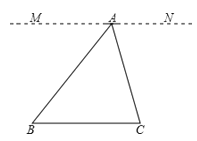
证明：过点作直线MN，使MN//BC.
∵MN∥BC，
∴∠B=∠MAB，∠C=∠NAC（两直线平行，内错角相等）
又∵∠MAB+∠NAC+∠BAC=180°（平角定义）
∴∠B+∠C+∠BAC=180°（等量代换）即∠A+∠B+∠C=180°.
故答案为：三角形的内角和是180°；∠A+∠B+∠C=180°；证明见解析.
练习册系列答案
一线名师权威作业本系列答案
相关题目
【题目】某校七（1）班体育委员统计了全班同学60秒跳绳的次数，并绘制出如下频数分布表和频数分布直方图：
次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | a | 4 | 12 | 16 | 8 | 3 |
结合图表完成下列问题：
（1）a= ，全班人数是______；
（2）补全频数分布直方图；
（3）若跳绳次数不少于140的学生成绩为优秀，则优秀学生人数占全班总人数的百分之几？
