题目内容
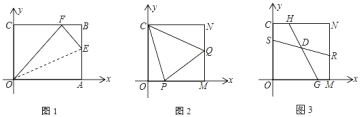
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
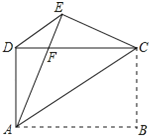
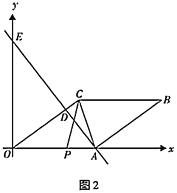
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
【答案】(1)AE=5;(2)见解析;(3)![]() .
.
【解析】
(1)设![]() ,在
,在![]() 中,根据勾股定理列方程解出即可;
中,根据勾股定理列方程解出即可;
(2)作辅助线,构建两个三角形全等,证明![]() 和
和![]() ,由
,由![]() ,得出结论;
,得出结论;
(3)作辅助线,构建平行四边形和全等三角形,可得![]() 和
和![]() ,则
,则![]() ,
,![]() ,证明
,证明![]() 和
和![]() ,得
,得![]() ,设
,设![]() ,在
,在![]() 中,根据勾股定理列方程求出EN的长,再利用勾股定理求CE,则SR与CE相等,即可得出结论.
中,根据勾股定理列方程求出EN的长,再利用勾股定理求CE,则SR与CE相等,即可得出结论.
(1)如图1,由题意得:![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ,
,
∴![]() ;
;
(2)如图2,在PO的延长线上取一点E',使![]() ,
,
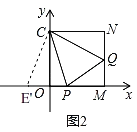
∵![]() ,
,![]() ,
,
∴四边形OMNC是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②如图3,过C作![]() ,在x轴负半轴上取一点E′,使
,在x轴负半轴上取一点E′,使![]() ,得
,得![]() ,
,
且![]() ,则
,则![]() ,
,
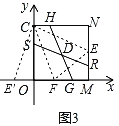
过C作![]() 交OM于F,连接FE,得
交OM于F,连接FE,得![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,
解得:![]() ,
,
∴![]() ,
,
根据勾股定理得:![]() ,
,
∴![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】二次函数y= ax+bx+c,自变量x 与函数y 的对应值如表:
x | ... | -5 | -4 | -3 | -2 | -1 | 0 | ... |
y | ... | 4 | 0 | -2 | -2 | 0 | 4 | ... |
下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是x=-5/2