题目内容
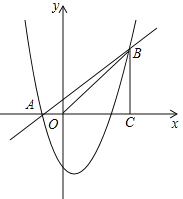
【题目】如图,已知抛物线![]() 经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
【答案】(1)数量关系![]() (2)
(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】试题分析:(1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c求出b和c的值即可;
(2)过点O作OH⊥AB,垂足为H,根据勾股定理可求出AB的长,进而得到:在Rt△BOH中,tan∠ABO=![]() .
.
(3)设点M的坐标为(x,x2-2x-3),点N的坐标为(x,x+1),在分两种情况:当点M在点N的上方时和当点M在点N的下方时,则四边形NMCB是平行四边形讨论求出符合题意的点M的横坐标即可.
试题解析::(1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c,得
![]() ,
,
解得b=-2,c=-3.
∴抛物线的解析式:y=x2-2x-3.
(2)在Rt△BOC中,OC=4,BC=5.
在Rt△ACB中,AC=AO+OC=1+4=5,
∴AC=BC.
∴∠BAC=45°,AB=![]() .
.
如图1,过点O作OH⊥AB,垂足为H.
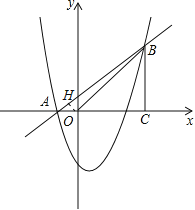
在Rt△AOH中,OA=1,
∴AH=OH=OA×sin45°=1×![]() =
=![]() ,
,
∴BH=AB-AH=![]() ,
,
在Rt△BOH中,tan∠ABO=![]() .
.
(3)直线AB的解析式为:y=x+1.
设点M的坐标为(x,x2-2x-3),
点N的坐标为(x,x+1),
如图2,当点M在点N的上方时,
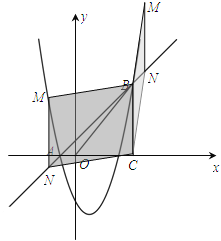
则四边形MNCB是平行四边形,MN=BC=5.
由MN=(x2-2x-3)-(x+1)=x2-2x-3-x-1=x2-3x-4,
解方程x2-3x-4=5,得x=![]() 或x=
或x=![]() .
.
②如图3,当点M在点N的下方时,则四边形NMCB是平行四边形,NM=BC=5.
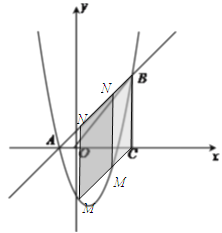
由MN=(x+1)-(x2-2x-3)=x+1-x2+2x+3=-x2+3x+4,
解方程-x2+3x+4=5,得x=![]() 或x=
或x=![]() .
.
所以符合题意的点M有4个,其横坐标分别为:![]() 、
、![]() 、
、![]() 、
、![]() .
.