Question

【题目】在学习了正方形后，数学小组的同学对正方形进行了探究，发现：

（1）如图1，在正方形ABCD中，点E为BC边上任意一点（点E不与B、C重合），点F在线段AE上，过点F的直线MN⊥AE，分别交AB、CD于点M、N . 此时，有结论AE=MN，请进行证明；

（2）如图2：当点F为AE中点时，其他条件不变，连接正方形的对角线BD， MN 与BD交于点G，连接BF，此时有结论：BF= FG，请利用图2做出证明.

（3）如图3：当点E为直线BC上的动点时，如果（2）中的其他条件不变，直线MN分别交直线AB、CD于点M、N，请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

图1 图2 图3

Answer 1

【答案】（1）证明见解析；

（2）证明见解析；

（3）AE与 MN的数量关系是：AE= MN ，BF与FG的数量关系是： BF= FG

【解析】（1）作辅助线，构建平行四边形PMND，再证明△ABE≌△DAP，即可得出结论；

（2）连接AG、EG、CG，构建全等三角形和直角三角形，证明AG=EG=CG，再根据四边形的内角和定理得∠AGE=90°，在R△AGE中，利用直角三角形斜边上的中线等于斜边的一半得BF=AE，FG=AE，则BF=GF；

（3）①AE=MN，证明△AEB≌△NMQ；

②BF=FG，同理得出BF和FG分别是直角△AEB和直角△AGF斜边上的中线，则 BF=AE，FG=AE，所以BF=FG.

证明：

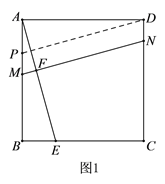
(1)在图1中，过点D作PD∥MN交AB于P，则∠APD=∠AMN

∵ 正方形ABCD

∴ AB = AD，AB∥DC，∠DAB =∠B = 90°

∴ 四边形PMND是平行四边形且PD = MN

∵ ∠B = 90° ∴∠BAE＋∠BEA= 90°

∵MN⊥AE于F， ∴∠BAE＋∠AMN = 90°

∴∠BEA =∠AMN =∠APD

又∵AB = AD，∠B =∠DAP = 90°

∴△ABE ≌ △DAP∴ AE = PD = MN

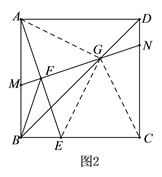
（2）在图2中连接AG、EG、CG

由正方形的轴对称性 △ABG ≌ △CBG∴ AG = CG，∠GAB=∠GCB

∵ MN⊥AE于F，F为AE中点∴ AG = EG

∴ EG = CG，∠GEC=∠GCE∴ ∠GAB=∠GEC

由图可知∠GEB＋∠GEC=180°∴ ∠GEB＋∠GAB =180°

又∵四边形ABEG的内角和为360°，∠ABE= 90°∴ ∠AGE = 90°

在Rt△ABE 和Rt△AGE中，AE为斜边，F为AE的中点，

∴BF=AE， FG= AE ∴BF= FG

（3）AE与 MN的数量关系是：AE= MN

BF与FG的数量关系是： BF= FG

“点睛”本题是四边形的综合题，考查了正方形、全等三角形、平行四边形的性质与判定，在有中点和直角三角形的前提下，可以利用直角三角形斜边上的中线等于斜边的一半来证明两条线段相等.