��Ŀ����
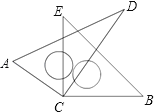
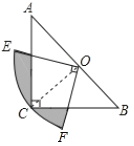
����Ŀ����֪��һ�����ǰ壨ֱ�����ǰ�OAB��ֱ�����ǰ�OCD����AOB=90�㣬��ABO=45�㣬��CDO=90�㣬��COD=60�㣩
��1����ͼ1�ڷţ���O��A��C��һֱ���ϣ����BOD�Ķ����Ƕ��٣�
��2����ͼ2����ֱ�����ǰ�OCD�Ƶ�O��ʱ�뷽��ת������ҪOBǡ��ƽ�֡�COD�����AOC�Ķ����Ƕ��٣�
��3����ͼ3�������ǰ�OCD�ڷ��ڡ�AOB�ڲ�ʱ��������OMƽ�֡�AOC������ONƽ�֡�BOD��������ǰ�OCD�ڡ�AOB���Ƶ�O����ת������MON�Ķ����Ƿ����仯��������䣬����ֵ������仯��˵�����ɣ�

���𰸡���1��30�㣻(2) 60�㣻(3) ����75��
��������
�������ǰ�ǵ������ͽ�ƽ���ߵĶ�����
��1��������ǵĶ��弴�ɵõ����ۣ�
��2���ɽ�ƽ���ߵĶ���õ���BOC=![]() ��COD=
��COD=![]() ��60��=30����������ǵĶ��弴�ɵõ����ۣ�
��60��=30����������ǵĶ��弴�ɵõ����ۣ�
��3�����ݽ�ƽ���ߵĶ���õ�![]() ����BOD+��AOC��=
����BOD+��AOC��=![]() ��30��=15����Ȼ����ݽǵĺͲ�ɵõ������
��30��=15����Ȼ����ݽǵĺͲ�ɵõ������
�⣺��1��![]() ��
��
��2����BOC=![]() ��COD=
��COD=![]() ��60��=30�㣬
��60��=30�㣬
���AOC=��AOB����BOC=90�㩁30��=60�㣻
��3����BOD+��AOC=90�㩁��COD=90�㩁60��=30�㣬
![]() ����BOD+��AOC��=
����BOD+��AOC��=![]() ��30��=15�㣬
��30��=15�㣬
��MON=![]() ����BOD+��AOC��+��COD=15��+60��=75��
����BOD+��AOC��+��COD=15��+60��=75��
����MON�Ķ������ᷢ���仯������75�㣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�