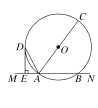题目内容
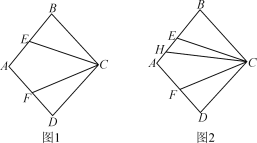
【题目】如图1,在菱形ABCD中,点E,F分别为AB,AD的中点,连结CE,CF.
(1)求证:CE=CF;
(2)如图2,若H为AB上一点,连结CH,使∠CHB=2∠ECB,求证:CH=AH+AB.
【答案】(1)见解析;(2)见解析
【解析】
(1)由菱形ABCD中,点E、F分别为AB、AD的中点,易证得△BCE≌△DCF(SAS),则可得CE=CF;
(2)由平行线的性质,可得AG=AB,∠G=∠FCD,由全等三角形的对应角相等,可得∠BCE=∠DCF,然后由∠CHB=2∠ECB,易证得∠G=∠HCG,则可得CH=GH,则可证出结果.
(1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,
∵点E、F分别为AB、AD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() AD,
AD,
∴BE=DF,
在△BCE和△DCF中,
 ,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;
(2)证明:延长BA与CF,交于点G,

∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,AF∥BC,AB∥CD,
∴∠G=∠FCD,
∵点F分别为AD的中点,且AG∥CD,
∴AG=AB,
∵△BCE≌△DCF,
∴∠ECB=∠DCF,
∵∠CHB=2∠ECB,
∴∠CHB=2∠G,
∵∠CHB=∠G+∠HCG,
∴∠G=∠HCG,
∴GH=CH,
∴CH=AH+AG=AH+AB.

练习册系列答案
相关题目