题目内容
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
【答案】(1)3;5;1或5;(2)6(3)9
【解析】
试题(1)根据数轴,观察两点之间的距离即可解决;
(2)根据|a+4|+|a-2|表示数a的点到-4与2两点的距离的和即可求解.
试题解析:(1)3;5;1或5;
(2)∵![]() 表示数轴上数
表示数轴上数![]() 和数-4,2之间距离的和,又因为
和数-4,2之间距离的和,又因为![]() 位于-4,2之间,
位于-4,2之间,
∴![]() 等于-4,2之间的距离和,
等于-4,2之间的距离和,
即![]() =|2-(-4)|=6.
=|2-(-4)|=6.
(3)∵![]() 表示数轴上数
表示数轴上数![]() 和数-5,1,4之间距离的和,
和数-5,1,4之间距离的和,
∴a=1时距离的和最小
∴![]() =
=![]() =|4-(-5)|=9
=|4-(-5)|=9

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE. 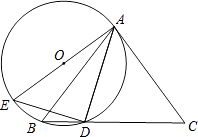
(1)求证:AC是⊙O的切线;
(2)若sinC= ![]() ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.