题目内容
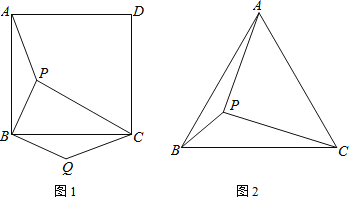
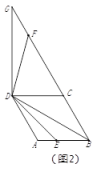
【题目】如图,直线y=kx+b过x轴上的点A(2,0),且与抛物线![]() 交于B,C两点,点B坐标为(1,1).
交于B,C两点,点B坐标为(1,1).
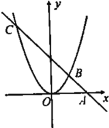
(1)求直线与抛物线对应的函数表达式;
(2)当![]() 时,请根据图象写出自变量x的取值范围;
时,请根据图象写出自变量x的取值范围;
(3)抛物线上是否存在一点D,使![]() ?若存在,求出D点坐标;若不存在,请说明理由
?若存在,求出D点坐标;若不存在,请说明理由
【答案】(1)y=x+2,y=x2(2)-2<x<1(3) (![]() ,3)或(
,3)或(![]() ,3)
,3)
【解析】
(1)已知直线AB经过A(2,0),B(1,1),设直线表达式为y=ax+b,可求直线解析式;将B(1,1)代入抛物线y=ax2可求抛物线解析式;
(2)求出B,C的坐标,根据图像即可求解;
(3)已知A,B,C三点坐标,根据作差法可求△OBC的面积,在△DOA中,已知面积和底OA,可求OA上的高,即D点纵坐标,代入抛物线解析式求横坐标,得出D点坐标.
(1)设直线AB关系式为y=kx+b
∵A(2,0),B(1,1)都在直线y=kx+b的图象上,
∴![]() 解得
解得![]() ,
,
∴直线AB关系式为y=x+2,
∵点B(1,1)在y=ax2的图象上,
∴a=1,其关系式为y=x2;
(2)由题意得![]() ,
,
解得![]() 或
或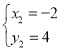
∴C(-2,4)
由图像可知![]() 表示一次函数在二次函数上方,
表示一次函数在二次函数上方,
故x的取值为-2<x<1;
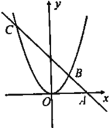
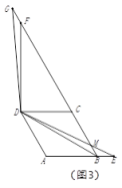
(3)如图,存在点D,设D(x,x2),
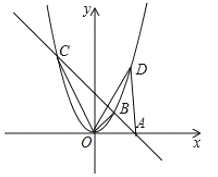
∴S△OAD=![]() |OA||yD|=
|OA||yD|=![]() ×2×x2=x2
×2×x2=x2
∵C(2,4),
∴S△BOC=S△AOCS△OAB=![]() ×2×4
×2×4![]() ×2×1=3,
×2×1=3,
∵S△BOC=S△OAD,
∴x2=3,
解得x=±![]() ,
,
∴点D坐标为(![]() ,3)或(
,3)或(![]() ,3).
,3).

【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③