题目内容
【题目】如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
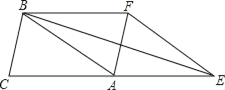
【答案】(1)9;(2)BE⊥AF,理由详见解析;(3)![]() ;
;
【解析】
(1)根据题意可得△ABC≌△EFA,BA∥EF,且BA=EF,根据一组对边平行且相等的四边形为平行四边形即可判定四边形AFBC为平行四边形,所以S△EFA=S△BAF=S△ABC=3,即可求得四边形EFBC的面积为9;(2))BE⊥AF,证明四边形EFBA为菱形,根据菱形的性质即可证得结论;(3)如上图,作BD⊥AC于D,已知∠BEC=15°,AE=AB,根据等腰三角形的性质可得∠EBA=∠BEC=15°,由三角形外角的性质可得∠BAC=2∠BEC=30°,在Rt△BAD中,AB=2BD,设BD=x,则AC=AB=2x,根据三角形的面积公式S△ABC=![]() ACBD列出方程,解方程求得x的值,即可求得AC的长.
ACBD列出方程,解方程求得x的值,即可求得AC的长.
(1)由平移的性质得,
AF∥BC,且AF=BC,△EFA≌△ABC,
∴四边形AFBC为平行四边形,
S△EFA=S△BAF=S△ABC=3,
∴四边形EFBC的面积为9;
(2)BE⊥AF,
由(1)知四边形AFBC为平行四边形,
∴BF∥AC,且BF=AC,
又∵AE=CA,
∴四边形EFBA为平行四边形,
又∵AB=AC,
∴AB=AE,
∴平行四边形EFBA为菱形,
∴BE⊥AF;
(3)如上图,作BD⊥AC于D,
∵∠BEC=15°,AE=AB,
∴∠EBA=∠BEC=15°,
∴∠BAC=2∠BEC=30°,
∴在Rt△BAD中,AB=2BD,
设BD=x,则AC=AB=2x,
∵S△ABC=3,且S△ABC=![]() ACBD=
ACBD=![]() 2xx=x2,
2xx=x2,
∴x2=3,
∵x为正数,
∴x=![]() ,
,
∴AC=2![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:g) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
这批样品的平均质量比标准质量多还是少?多或少几克?若每袋标准质量为500克,则抽样检测的总质量是多少?