题目内容
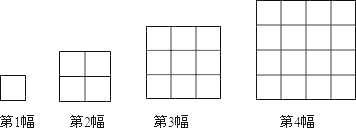
【题目】如图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有1+4＝5个正方形；第三幅图中有1+4+9＝14个正方形；…按这样的规律下去，第4幅图中有_____个正方形．
【答案】30
【解析】
观察图形发现：第1幅图中有1个正方形，第2幅图中有1+4=5个正方形，第3幅图中有1+4+9=14个正方形，…由此得出第n幅图中有12+22+32+42+…+n2＝
n（n+1）（2n+1）个正方形从而得到答案．
解：∵第1幅图中有1个正方形，
第2幅图中有1+4＝5个正方形，
第3幅图中有1+4+9＝14个正方形，
…
∴第n幅图中有12+22+32+42+…+n2＝n（n+1）（2n+1），
∴第4幅图中有12+22+32+42＝30个正方形．
故答案为30．
练习册系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两班各推选10名同学进行投篮比赛，按照比赛规则，每人各投了10个球，两个班选手的进球数统计如表，请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
（1）分别写出甲、乙两班选手进球数的平均数、中位数与众数；
（2）如果要从这两个班中选出一个班级参加学校的投篮比赛，争取夺得总进球团体的第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？
【题目】如图，搭第一个图形需要
根火柴棒．
（1）搭一搭，填一填：
三角形个数 |
|
|
|
|
| … |
火柴棒根数 | … |
（2）搭
个这样的三角形需要________根火柴棒．
（3）搭40个这样的三角形需要________根火柴棒．
（4）搭
个这样的三角形需要________根火柴棒．