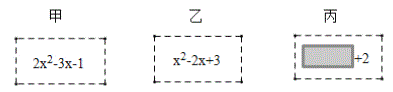题目内容
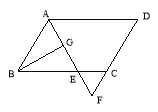
【题目】如图,在平行四边形ABCD中,AB=12,AD=18,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长是 .
,则△CEF的周长是 .
【答案】16.
【解析】
试题分析:先计算出△ABE的周长,然后根据相似比的知识进行解答即可.
∵在ABCD中,AB=CD=12,AD=BC=18,∠BAD的平分线交BC于点E,
∴△ADF是等腰三角形,AD=DF=18;
∵AB=BE=12,
∴CF=6;
∴在△ABG中,BG⊥AE,AB=12,BG=![]() ,
,
可得:AG=4,
又∵BG⊥AE,
∴AE=2AG=8,
∴△ABE的周长等于32,
又∵ABCD,
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为16.
故答案为16.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目