题目内容
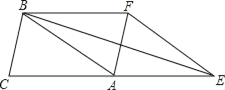
【题目】如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,则下列结论:①OG=![]() AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
AB;②图中与△EGD全等的三角形共有5个;③以点A、B、D、E为项点的四边形是菱形;④S四边形ODGF=S△ABF.其中正确的结论是( )
A. ①③B. ①③④C. ①②③D. ②②④
【答案】A
【解析】
由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=![]() CD=
CD=![]() AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=
AB,①正确;先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,③正确;由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;证出OG是△ABD的中位线,得出OG//AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;④不正确;即可得出结果.
解:四边形ABCD是菱形,

在△ABG和△DEG中,
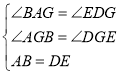
∴△ABG≌△DEG(AAS),
∴.AG=DG,
∴OG是△ACD的中位线,
∴OG=![]() CD=
CD=![]() AB,①正确;
AB,①正确;
∵AB//CE,AB=DE,
∴四边形ABDE是平行四边形,
∴∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,③正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
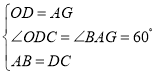
∴△ABG≌△DCO
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,则②不正确。
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=![]() △ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴ S四边形ODGF=S△ABF;④不正确;
故答案为:A.