��Ŀ����
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�������![]() �����
�����![]() ��������
��������![]() .
.

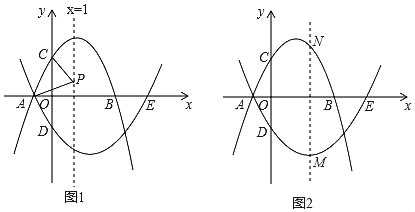
��1��ֱ��д��![]() �����꣨______��______����
�����꣨______��______����![]() �����꣨______��______����
�����꣨______��______����
��2����ͼ��DΪ![]() �е�.����
�е�.����![]() ��
��![]() ������ڵڶ���������һ��
������ڵڶ���������һ��![]() �����ı���
�����ı���![]() �������
�������![]() �����
�����![]() ���������������ĵ�
���������������ĵ�![]() �����ꣻ
�����ꣻ

��3����ͼ������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ٶ����߶�
����λ���ٶ����߶�![]() �˶���ͬʱ����
�˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ����.��ÿ��
����.��ÿ��![]() ����λ���B�����߶�
����λ���B�����߶�![]() �˶�����
�˶�����![]() ����
����![]() ��ʱ��
��ʱ��![]() ��
��![]() ͬʱֹͣ�˶����˶�ʱ����
ͬʱֹͣ�˶����˶�ʱ����![]() ��
��![]() ����
����![]() ��
��![]() �˶�������.��
�˶�������.��![]() ʱ��ֱ��д��ʱ��
ʱ��ֱ��д��ʱ��![]() ��ֵ.
��ֵ.

���𰸡���1��![]() ��
��![]() ��2��
��2��![]() ��3��
��3��![]() ��
��![]()
��������
��1�����ݾ��ε����ʺ�ֱ������ϵ�е��ȷ�����������![]() �������
�������![]() �����ꣻ
�����ꣻ
��2�������ı���![]() �������
�������![]() �����
�����![]() �����г�����m�ķ��̣��ⷽ�̼��������
�����г�����m�ķ��̣��ⷽ�̼��������![]() �����ꣻ
�����ꣻ
��3���������ʾ��ON=6��2t��MC=t������M��ON �ô���ME��OA �ڵ�E��
���ݹ��ɶ����г�����t�ķ��̣���⼴��.
��1���߳�����![]() �����
�����![]() ��������
��������![]() ��
��
��BC=6��AB=4��
��OA=6��OC=4��
��A��6,0��C��0,4����
��2������PD��PO������P��PE��OD����OD �ڵ�E��
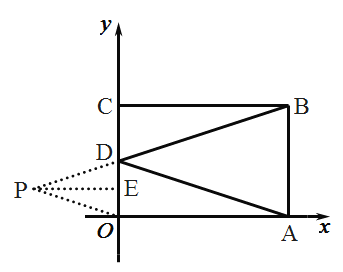
��BC=6��AB=4��
��![]() ��
��
���ı���![]() �������
�������![]() �����
�����![]() ����
����
���ı���![]() �������24��
�������24��
��![]()
![]()
��DΪ![]() �е㣬
�е㣬
��OD=2;
��![]() �ǵڶ����ĵ㣬
�ǵڶ����ĵ㣬
��PE=��m��
����з���Ϊ![]() �����m=��18��
�����m=��18��
��![]()
��3����ͼ������M��ON �Ĵ���ME��OA �ڵ�E��
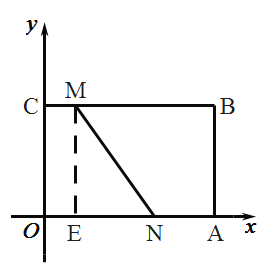
�������ON=6��2t��MC=t![]() ��
��
��ME=4��EN=6��3t
�֡�![]() ��
��
����ݹ��ɶ������з���Ϊ![]() ���ⷽ�̵�t=
���ⷽ�̵�t=![]() ��t=
��t=![]()
�൱t=![]() ��t=
��t=![]() ʱ��
ʱ��![]() .
.

 ������ϵ�д�
������ϵ�д�