��Ŀ����
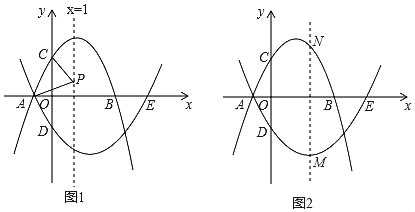
����Ŀ����ͼ1��������l1��y=��x2+bx+3��x���ڵ�A��B������A�ڵ�B����ࣩ����y���ڵ�C����Գ���Ϊx=1��������l2������A����x�����һ������ΪE��5��0������y���ڵ�D��0����5����
��1����������l2�ĺ�������ʽ��
��2��PΪֱ��x=1��һ���㣬����PA��PC����PA=PCʱ�����P�����ꣻ
��3��MΪ������l2��һ���㣬����M��ֱ��MN��y�ᣨ��ͼ2��ʾ������������l1�ڵ�N�����M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵ��
���𰸡���1��������l2�ĺ�������ʽ��y=x2��4x��5����2��P������Ϊ��1��1������3���ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12.5��
��������
��1����������l1�ĶԳ������b��ֵ�����ɵó�������l1�Ľ���ʽ���Ӷ��ó���A����B�����꣬�ɵ�B����E����D���������������l2�Ľ���ʽ���ɣ���2����CH��PG��ֱ��PG�ڵ�H�����P������Ϊ��1��y���������C�����꣬�����ó�CH=1��PH=|3��y |��PG=|y |��AG=2����PA=PC�ɵ�PA2=PC2���ɹ��ɶ����ֱ�PA2��PC2��CH��PH��PG��AG��ʾ���з������y��ֵ���ɣ���3�������M�����꣬������������߽���ĺ�����ֱ�Ϊ��1��4���ٵ���1��x��4ʱ����Mλ�ڵ�N���·�����ʾ��MN�ij���Ϊ����x�Ķ��κ�������x�ķ�Χ������κ�������ֵ���ڵ�4��x��5ʱ����Mλ�ڵ�N���Ϸ���ͬ�������ʱMN�����ֵ��ȡ���߽ϴ�ֵ�����ɵó�MN�����ֵ.
��1����������l1��y=��x2+bx+3�Գ���Ϊx=1��
��x=��![]() =1��b=2��
=1��b=2��
��������l1�ĺ�������ʽΪ��y=��x2+2x+3��
��y=0ʱ����x2+2x+3=0��
��ã�x1=3��x2=��1��
��A����1��0����B��3��0����
��������l2�ĺ�������ʽ��y=a��x��5����x+1����
��D��0����5��������5a=��5��a=1��
��������l2�ĺ�������ʽ��y=x2��4x��5��
��2����CH��PG��ֱ��PG�ڵ�H��
��P������Ϊ��1��y�����ɣ�1���ɵ�C������Ϊ��0��3����
��CH=1��PH=|3��y |��PG=|y |��AG=2��
��PC2=12+��3��y��2=y2��6y+10��PA2= =y2+4��
��PC=PA��
��PA2=PC2��
��y2��6y+10=y2+4�����y=1��
��P��������1��1����
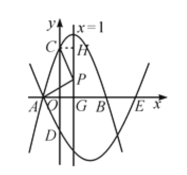
��3�����������M��x��x2��4x��5����
��MN��y�ᣬ
��N��x����x2+2x+3����
�x2+2x+3=x2��4x��5���ɽ��x=��1��x=4��
�ٵ���1��x��4ʱ��MN=����x2+2x+3������x2��4x��5��=��2x2+6x+8=��2��x��![]() ��2+
��2+![]() ��
��
��Ȼ��1��![]() ��4��
��4��
�൱x=![]() ʱ��MN�����ֵ12.5��
ʱ��MN�����ֵ12.5��
�ڵ�4��x��5ʱ��MN=��x2��4x��5��������x2+2x+3��=2x2��6x��8=2��x��![]() ��2��
��2��![]() ��
��
��Ȼ��x��![]() ʱ��MN��x�����������
ʱ��MN��x�����������
�൱x=5ʱ��MN�����ֵ��MN=2��5��![]() ��2��
��2��![]() =12.
=12.
���Ͽ�֪���ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12.5��

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�����Ŀ���ס��ҡ�����λ�˶�Ա����ͬ�����¸����![]() �Σ�ÿ����еijɼ����£�
�Σ�ÿ����еijɼ����£�
�ף�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�ң�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��1������������������±���
ƽ���� | ��λ�� | ���� | |
�� |
|
| __________ |
�� | __________ |
|
|
�� |
| __________ |
|
��2�����ݱ������ݷ�������λ�˶�Ա�ijɼ����ȶ�.����Ҫ˵������.
����Ŀ��ijѧУ���꼶���������࣬���μ���ѧУ���е��鷨�滭��������������ݳ����ɼ��ֱ�ѡ����10��ͬѧ�μӾ�������Щѡ�ֵľ����ɼ�(����100��)���±���ʾ��
�����ɼ�(��λ����) | |
����1�� | 80����86����88����80����88����99����80����74����91����89 |
����2�� | 85����85����87����97����85����76����88����77����87����88 |
����3�� | 82����80����78����78����81����96����97����87����92����84 |
����������⣺
(1)��������
ƽ����(��) | ����(��) | ��λ��(��) | |
������1�� | 85.5 | �� �� | 87 |
������2�� | 85.5 | 85 | �� �� |
������3�� | �� �� | 78 | 83 |
(2)�������������ͬ�ĽǶȶ������༶�ľ����ɼ�����
����ƽ�������������Ͽ�(�����ĸ��༶�ɼ���Щ)��
����ƽ��������λ�����Ͽ�(�����ĸ��༶�ɼ���Щ)��
(3)�����ÿ���༶�μӾ�����ѡ���зֱ�ѡ��3�˲μ��ܾ���������Ϊ�ĸ��༶��ʵ����ǿһЩ�����Ҫ˵�����ɣ�



