题目内容
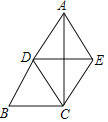
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

【答案】∠1+∠2=180°
【解析】
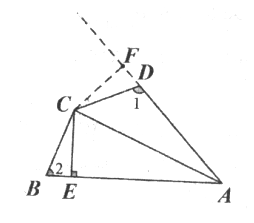
延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件![]() ,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
猜想:∠1+∠2=180°
证明:过C点作CF⊥AD延长线于点F,
∵CE⊥AB,AC平分∠DAB,
∴CB=CF,
∠CEB=∠CFD=90°,
在Rt△CEA和Rt△CFA中
∵![]()
∴Rt△CEA≌Rt△CFA(HL),
∴AE=AF,
∵![]() ,
,
AE+AF=AF-FD+AE+BE,
∴FD=BE,
在△CEB和△CFD中
∵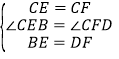
∴△CEB≌△CFD(SAS),
∴∠2=∠CDF,
∵∠CDF+∠1=180°,
∴∠1+∠2=180°.

练习册系列答案
相关题目