题目内容
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2013年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
【答案】
(1)解:设平均增长率为a,根据题意得:
64(1+a)2=100
解得:a=0.25=25%或a=﹣2.25
四月份的销量为:100(1+25%)=125(辆).
答:四月份的销量为125辆
(2)解:设购进A型车x辆,则购进B型车 ![]() 辆,
辆,
根据题意得:2× ![]() ≤x≤2.8×
≤x≤2.8× ![]()
解得:30≤x≤35
利润W=(700﹣500)x+ ![]() (1300﹣1000)=9000+50x.
(1300﹣1000)=9000+50x.
∵50>0,∴W随着x的增大而增大.
当x=35时, ![]() 不是整数,故不符合题意,
不是整数,故不符合题意,
∴x=34,此时 ![]() =13(辆).
=13(辆).
答:为使利润最大,该商城应购进34辆A型车和13辆B型车
【解析】(1)首先根据1月份和3月份的销售量求得月平均增长率,然后求得4月份的销量即可;(2)设A型车x辆,根据“A型车不少于B型车的2倍,但不超过B型车的2.8倍”列出不等式组,求出x的取值范围;然后求出利润W的表达式,根据一次函数的性质求解即可.

【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表: 甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图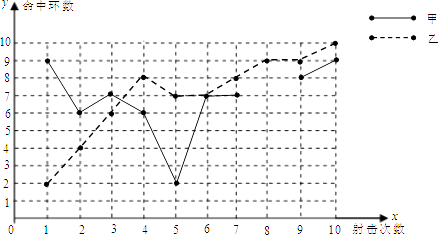
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?