Question

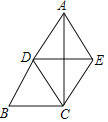
【题目】已知：如图，在△ABC中，∠ACB=90°，点D是斜边AB的中点，DE∥BC，且CE=CD．

（1）求证：∠B=∠DEC；

（2）求证：四边形ADCE是菱形．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

(1)根据直角三角形斜边上的中线等于斜边的一半，得到DB=DC，从而∠B=∠DCB，由DE∥BC，得到∠DCB=∠CDE，由CE=CD，得到∠CDE=∠DEC，利用等量代换，得到∠B=∠DEC；

(2)先利用一组对边平行且相等的四边形是平行四边形，证明四边形ADCE是平行四边形，再由CD=CE，证明平行四边形ADCE是菱形.

（1）证明：在△ABC中，∵∠ACB=90°，点D是斜边AB的中点，

∴CD=DB，

∴∠B=∠DCB，

∵DE∥BC，

∴∠DCB=∠CDE，

∵CD=CE，

∴∠CDE=∠CED，

∴∠B=∠CED．

（2）证明：∵DE∥BC，

∴∠ADE=∠B，

∵∠B=∠DEC，

∴∠ADE=∠DEC，

∴AD∥EC，

∵EC=CD=AD，

∴四边形ADCE是平行四边形，

∵CD=CE，

∴四边形ADCE是菱形．

故答案为：（1）证明见解析；（2）证明见解析.