题目内容
【题目】在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值= . 
【答案】4+2 ![]()
【解析】解:由题可得,点C在以AB为直径的⊙D上运动, 点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,
此时,直线y=﹣x+m与⊙D相切,交x轴与E,如图所示,
连接OD,CD,
∵A(6,0)、B(0,2),
∴D(3,1),
∴OD= ![]() =
= ![]() ,
,
∴CD= ![]() ,
,
根据两点间的距离可得,C(3+ ![]() ,1+
,1+ ![]() ),
),
代入直线y=﹣x+m,可得
1+ ![]() =﹣(3+
=﹣(3+ ![]() )+m,
)+m,
解得m=4+2 ![]() ,
,
∴x+y的最大值为4+2 ![]() ,
,
故答案为:4+2 ![]() .
.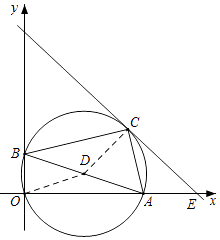
根据以AB为斜边在右上方作Rt△ABC,可知点C在以AB为直径的⊙D上运动,根据点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,此时,直线y=﹣x+m与⊙D相切,再根据圆心点D的坐标,可得C的坐标为(3+ ![]() ,1+
,1+ ![]() ),代入直线y=﹣x+m,可得m=4+2
),代入直线y=﹣x+m,可得m=4+2 ![]() ,即可得出x+y的最大值为4+2
,即可得出x+y的最大值为4+2 ![]() .
.

练习册系列答案
相关题目