题目内容
【题目】已知三角形的两边长分别为5和7，则第三边的中线长x的取值范围是（ ）
A. 
B. 
C. 
D. 无法确定
【答案】C
【解析】
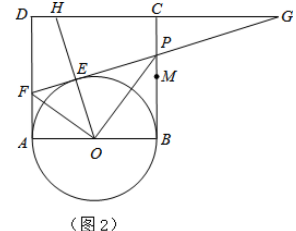
如图所示，延长中线AD使AD=ED，根据全等三角形的判定定理，可证明△BDE≌△CDA；由全等性质可知，BE=AC，所以由三边关系可得7-5＜AE＜7+5；再结合
，即可求出AD的取值范围.
根据题意画出图形△ABC中线为AD，延长AD使AD=DE.
∵AD是△ABC的中线，
∴BD=CD.
∵AD=ED，∠ADC=∠EDB，BD=CD，
∴△BDE≌△CDA，
∴BE=AC.
在三角形ABE中由三边关系得，7-5＜AE＜7+5.
∵AE是中线AD的2倍，
∴中线的取值范围为1＜AE＜6，即1＜x＜6.
故选:C.
练习册系列答案
相关题目
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表： 甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图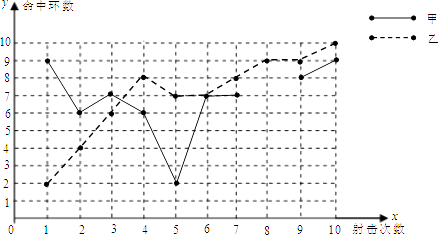
（1）请补全上述图表（请直接在表中填空和补全折线图）；
（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；
（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？
