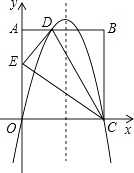
��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������y= ![]() x2��
x2�� ![]() x��2��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C����D���C����x��Գƣ�����BD
x��2��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C����D���C����x��Գƣ�����BD
��1�����A��B��C�����꣮
��2������Pʱx���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l�����������ڵ�M����ֱ��BD�ڵ�N
�ٵ���P���߶�OB���˶�ʱ������O��B�غϣ�����mΪ��ֵʱ���߶�MN�ij������˵����ʱ�ı���DCMN�Ƿ�Ϊƽ���ı���
�ڵ���P���˶������У��Ƿ���ڵ�M��ʹ��BDM����BDΪֱ�DZߵ�ֱ�������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��y= ![]() x2��
x2�� ![]() x��2�У���y=0�ɵ�0=
x��2�У���y=0�ɵ�0= ![]() x2��
x2�� ![]() x��2�����x=��1��x=4��
x��2�����x=��1��x=4��
��A����1��0����B��4��0����
��y= ![]() x2��
x2�� ![]() x��2�У���x=0�ɵ�y=��2��
x��2�У���x=0�ɵ�y=��2��
��C��0����2����
��2��
�١�D��C����x��Գƣ�
��D��0��2������B��4��0����
�����ֱ��BD����ʽΪy=kx+2����B���������ɵ�4k+2=0�����k=�� ![]() ��
��
��ֱ��BD����ʽΪy=�� ![]() x+2��
x+2��
��P��m��0����
��N��m���� ![]() m+2����M��m��
m+2����M��m�� ![]() m2��
m2�� ![]() m��2����
m��2����
��P���߶�OB�ϣ�
��M��x���·���
��MN=�� ![]() m+2����
m+2���� ![]() m2��
m2�� ![]() m��2��=��
m��2��=�� ![]() m2+m+4=��
m2+m+4=�� ![]() ��m��1��2+
��m��1��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
�൱m=1ʱ��MN�����ֵ�����ֵΪ ![]() ��
��
��CD=4��MN��
���ı���DCMN����ƽ���ı��Σ�
�ڡߵ�P���߶�OB���˶���
���M�ڵ������ޣ�
���MDB��90�㣬
����BDM����BDΪֱ�DZߵ�ֱ��������ʱ��ֻ��MB��BD����ͼ��
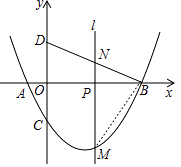
��P��m��0������M��m�� ![]() m2��
m2�� ![]() m��2������B��4��0����D��0��2����
m��2������B��4��0����D��0��2����
��BP=4��m��PM=�� ![]() m2+
m2+ ![]() m+2��OB=4��OD=2��
m+2��OB=4��OD=2��
�ߡ�MBD=90�㣬
���OBD+��PBM=��ODB+��OBD=90�㣬
���ODB=��PMB��
���OBD�ס�PMB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����m=3��m=4����ȥ����
�����m=3��m=4����ȥ����
��M��������3����2����
����������1�����������߽���ʽ�������A��B��C�����ꣻ��2���ٿ����ֱ��BD�Ľ���ʽ������m�ɱ�ʾ��MN�ij���������ö��κ������������MN�����ֵ�����ж�MN��CD�Ƿ���ȼ��ɣ����������ֻ֪��BM��BD�������M������꣬�Ӷ��ɱ�ʾ��BP��MP�ij������á�OBD�ס�PMB���ɵõ�����M������ķ��̣��Ӷ������M������꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���Լ���ƽ���ı��ε��ж������ʵ����⣬�˽���һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε������

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�