��Ŀ����
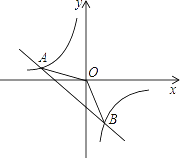
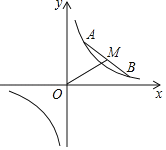
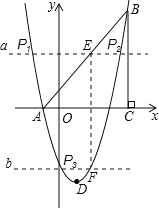
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A����1��0����C��4��0����BC��x���ڵ�C����AC��BC��������y��x2+bx+c����A��B���㣮
��1���������ߵı���ʽ��
��2����E���߶�AB��һ���㣨����A��B�غϣ�������E��x��Ĵ��ߣ����������ڵ�F�����߶�EF�ij������ʱ�����E�����ꣻ
��3���ڣ�2���������£������������Ƿ����һ��P��ʹ��EFP����EFΪֱ�DZߵ�ֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��y��x2��2x��3����2����E������Ϊ��![]() ��
��![]() ������3�����ڣ�P1��
������3�����ڣ�P1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ����P3��
����P3��![]() ��
��![]() ����
����
��������
��1������õ�A�����꣬Ȼ��A�͵�B��������������ߵĽ���ʽ�ɵõ�����b��c�ķ����飬�Ӷ������b��c��ֵ��
��2�����E������Ϊ��x��x+1�������F������ΪF��x��x2��2x��3������ɵõ�EF��x�ĺ�����ϵʽ�������䷽�������EF�����ֵ�Լ���E�����ꣻ
��3�����ڣ�������������ǣ���i������E��a��EF���������ڵ�P�����P��m��m2��2m��3������E����������P����������г�����m�ķ��̣�������̵Ľ�õ�m��ֵ��ȷ����P1��P2�����ꣻ����������F��b��EF����������P3����P3��n��n2��2n��3��������F����������P������������г�����n�ķ��̣�������̵Ľ�õ�n��ֵ�����P3�����꣬���ϵõ�������������P�����꣮
��1����A����1��0����C��4��0����
��OA��1��OC��4��
��AC��5��
��BC��x���ڵ�C����AC��BC��
��B��4��5����
����A�͵�B��������������ߵĽ���ʽ�ã�![]() ����ã�b����2��c����3��
����ã�b����2��c����3��
�������ߵĽ���ʽΪy��x2��2x��3��
��2����ֱ��AB������A����1��0����B��4��5����
��ֱ��AB�Ľ���ʽΪy��kx+b��
��![]() ����ã�
����ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪ��y��x+1��
�߶��κ���y��x2��2x��3��
�����E��t��t+1������F��t��t2��2t��3����
��EF����t+1������t2��2t��3��������t��![]() ��
��![]() ��
��
�൱t��![]() ʱ��EF�����ֵΪ
ʱ��EF�����ֵΪ![]() ��
��
���E��������![]() ����
����
��3�����ڣ�������������ǣ�
����������E��a��EF���������ڵ�P�����P��m��m2��2m��3����
��![]()
![]() ��
��
��m1=![]() ��m2=
��m2=![]()
��P1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ��
��
����������F��b��EF����������P3����P3��n��n2��2n��3��
����n2��2n��3����![]()
��n1=![]() , n2=
, n2=![]() ����ȥ��
����ȥ��
��P3��![]() ��
��![]() ����
����
����������ʹ��EFP����EFΪֱ�DZߵ�ֱ�����������е�P������Ϊ��P1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ����P3��
����P3��![]() ��
��![]() ����
����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ����У�ݸ���ѧ��Ϊ���˽�ѧ�������Ķ���������������˲���ѧ��ÿ�����ڿ����Ķ���ʱ�䣬�������£�
�����ռ�����ȫУ�����ȡ20��ѧ����������ÿ�����ڿ����Ķ�ʱ��ĵ��飬�������£���λ���֣�
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
�����·ֶ������������ݲ���ȫ����
�����Ķ�ʱ��x���֣� | 0��x��40 | 40��x��80 | 80��x��120 | 120��x��160 |
�ȼ� | D | C | B | A |
���� | 3 | �� �� | 8 | �� �� |
�������ݣ���ȫ���б����е�ͳ������
ƽ���� | ��λ�� | ���� |
80 | �� �� | �� �� |
�ó����ۣ�
��1���������е�ͳ����������Уѧ��ÿ�����ڿ����Ķ�ʱ�������ȼ�Ϊ�� ����
��2������ƽ���Ķ�һ���������ʱ��Ϊ160���ӣ�����ѡ�������е�ƽ����������Уѧ��ÿ��һ�꣨��52�ܼ��㣩ƽ���Ķ����ٱ������飿