Question

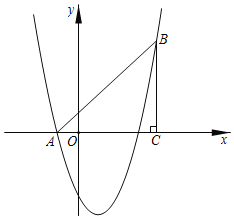
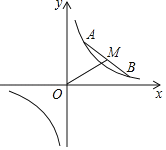
【题目】如图，在平面直角坐标系中，点，在反比例函数的图象上运动，且始终保持线段的长度不变．为线段的中点，连接．则线段长度的最小值是_____(用含的代数式表示)．

Answer 1

【答案】

【解析】

如图，当OM⊥AB时，线段OM长度的最小．首先证明点A与点B关于直线y=x对称，因为点A，B在反比例函数的图象上，AB=4，所以可以假设A（m，），则B（m+4，-4），则有=，解得k=m2+4m，推出A（m，m+4），B（m+4，m），可得M（m+2，m+2），求出OM即可解决问题．

如图，当时，线段长度的最小，

∵为线段的中点，

∴，

∵点，在反比例函数的图象上，

∴点与点关于直线对称，

∵，

∴可以假设，则，

∴，

解得，

∴，，

∴，

∴，

∴的最小值为．

故答案为．